Лекция 6. Нелинейные регрессионные модели

Полиномиальная множественная регрессионная модель

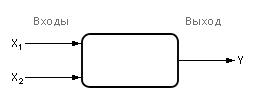
Рис. 6.1. Обозначение двумерной модели черного ящика на схемах

Если черный ящик имеет, например, два входа, а зависимость выхода от входов напоминает квадратичную, то целесообразно выбрать такую гипотезу:

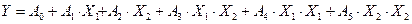
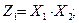
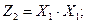
Обозначим: 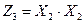и подставим эти выражения в предыдущую формулу:

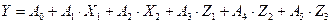
Таким образом, данная задача сведена к линейной множественной модели. А модель черного ящика теперь выглядит так, как показано на рис. 6.2.

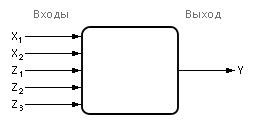
Рис. 6.2. Преобразованная модель черного ящика

Мультипликативная регрессионная модель

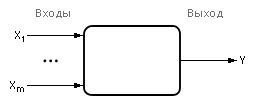
Рис. 6.3. Обозначение модели многомерного черного ящика на схемах

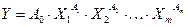
Прологарифмируем левую и правую части данного уравнения:

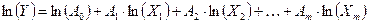
Обозначим:

W = ln(Y), B0 = ln(A0), Z1 = ln(X1), Z2 = ln(X2), …, Zm = ln(Xm).

Получим:

W = B0 + A1 · Z1 + A2 · Z2 + … + Am · Zm.

То есть вновь осуществлен переход к линейной множественной модели.

Обратная регрессионная модель

Рис. 6.4. Обозначение модели многомерного черного ящика на схемах

Y = k/(A0 + A1X1 + … + AmXm).

Заменим: W = 1/Y, ai = Ai/k. И перейдем к линейной множественной модели:

W = a0 + a1 · X1 + … + am · Xm.