Лекция 8. Статистическое моделирование
Статистическое моделирование — базовый метод моделирования, заключающийся в том, что модель испытывается множеством случайных сигналов с заданной плотностью вероятности. Целью является статистическое определение выходных результатов. В основе статистического моделирования лежит метод Монте-Карло. Напомним, что имитацию используют тогда, когда другие методы применить невозможно.
Метод Монте-Карло
Рассмотрим метод Монте-Карло на примере вычисления интеграла, значение которого аналитическим способом найти не удается.
Задача 1. Найти значение интеграла:

На рис. 8.1 представлен график функции 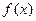 . Вычислить значение интеграла этой функции — значит, найти площадь под этим графиком.
. Вычислить значение интеграла этой функции — значит, найти площадь под этим графиком.
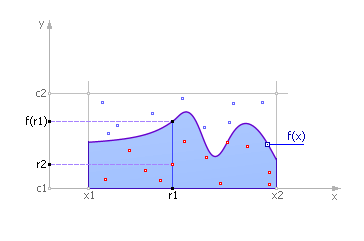
Рис. 8.1. Определение значения интеграла методом Монте-Карло
Ограничиваем кривую сверху, справа и слева. Случайным образом распределяем точки в прямоугольнике поиска. Обозначим через 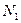 количество точек, принятых для испытаний (то есть попавших в прямоугольник, эти точки изображены на рис. 8.1 красным и синим цветом), и через
количество точек, принятых для испытаний (то есть попавших в прямоугольник, эти точки изображены на рис. 8.1 красным и синим цветом), и через 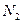 — количество точек под кривой, то есть попавших в закрашенную площадь под функцией (эти точки изображены на рис. 8.1 красным цветом). Тогда естественно предположить, что количество точек, попавших под кривую по отношению к общему числу точек пропорционально площади под кривой (величине интеграла) по отношению к площади испытуемого прямоугольника. Математически это можно выразить так:
— количество точек под кривой, то есть попавших в закрашенную площадь под функцией (эти точки изображены на рис. 8.1 красным цветом). Тогда естественно предположить, что количество точек, попавших под кривую по отношению к общему числу точек пропорционально площади под кривой (величине интеграла) по отношению к площади испытуемого прямоугольника. Математически это можно выразить так:
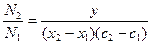
Рассуждения эти, конечно, статистические и тем более верны, чем большее число испытуемых точек мы возьмем.
Фрагмент алгоритма метода Монте-Карло в виде блок-схемы выглядит так, как показано на рис. 8.2.
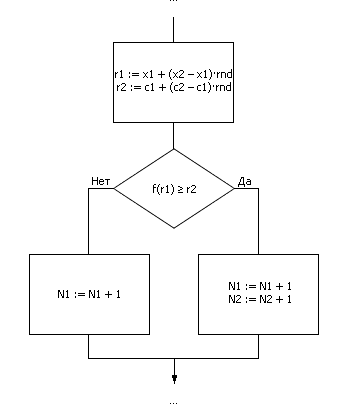
Рис. 8.2. Фрагмент алгоритма реализации метода Монте-Карло
Значения 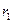 и
и 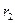 на рис. 8.2 являются равномерно распределенными случайными числами из интервалов
на рис. 8.2 являются равномерно распределенными случайными числами из интервалов 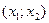 и
и 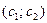 соответственно.
соответственно.
Метод Монте-Карло чрезвычайно эффективен, прост, но необходим «хороший» генератор случайных чисел. Вторая проблема применения метода заключается в определении объема выборки, то есть количества точек, необходимых для обеспечения решения с заданной точностью. Эксперименты показывают: чтобы увеличить точность в 10 раз, объем выборки нужно увеличить в 100 раз; то есть точность примерно пропорциональна корню квадратному из объема выборки:
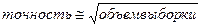
Дата добавления: 2015-12-08; просмотров: 956;
