Метод серединных квадратов

Имеется некоторое четырехзначное число R0. Это число возводится в квадрат и заносится в R1. Далее из R1 берется середина (четыре средних цифры) — новое случайное число — и записывается в R0. Затем процедура повторяется (см. рис. 22.6). Отметим, что на самом деле в качестве случайного числа необходимо брать не ghij, а 0.ghij — с приписанным слева нулем и десятичной точкой. Этот факт отражен как на рис. 22.6, так и на последующих подобных рисунках.

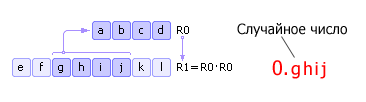
Рис. 9.6. Схема метода серединных квадратов

Недостатки метода: 1) если на некоторой итерации число R0 станет равным нулю, то генератор вырождается, поэтому важен правильный выбор начального значения R0; 2) генератор будет повторять последовательность через Mⁿ шагов (в лучшем случае), где n — разрядность числа R0, M — основание системы счисления.

Для примера на рис. 9.6: если число R0 будет представлено в двоичной системе счисления, то последовательность псевдослучайных чисел повторится через 2⁴ = 16 шагов. Заметим, что повторение последовательности может произойти и раньше, если начальное число будет выбрано неудачно.

Описанный выше способ был предложен Джоном фон Нейманом и относится к 1946 году. Поскольку этот способ оказался ненадежным, от него очень быстро отказались.

Метод серединных произведений

Число R0 умножается на R1, из полученного результата R2 извлекается середина R2^* (это очередное случайное число) и умножается на R1. По этой схеме вычисляются все последующие случайные числа (см. рис. 9.7).

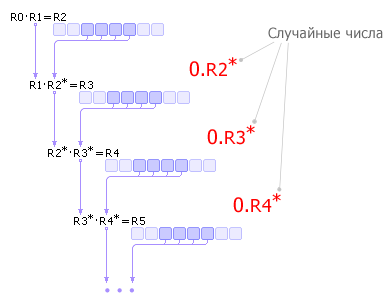
Рис. 9.7. Схема метода серединных произведений