Проверка качества работы генератора

От качества работы ГСЧ зависит качество работы всей системы и точность результатов. Поэтому случайная последовательность, порождаемая ГСЧ, должна удовлетворять целому ряду критериев.

Осуществляемые проверки бывают двух типов:

• проверки на равномерность распределения;
• проверки на статистическую независимость.

Проверки на равномерность распределения

1) ГСЧ должен выдавать близкие к следующим значения статистических параметров, характерных для равномерного случайного закона:

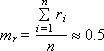
— математическое ожидание;

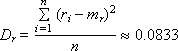
— дисперсия;

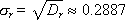
— среднеквадратичное отклонение.

Частотный тест

Частотный тест позволяет выяснить, сколько чисел попало в интервал (m_r – σ_r; m_r + σ_r), то есть (0.5 – 0.2887; 0.5 + 0.2887) или, в конечном итоге, (0.2113; 0.7887). Так как 0.7887 – 0.2113 = 0.5774, заключаем, что в хорошем ГСЧ в этот интервал должно попадать около 57.7% из всех выпавших случайных чисел (см. рис. 9.9).

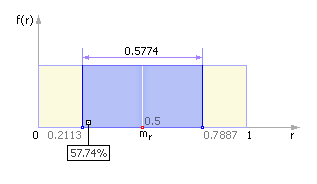
Рис. 9.9. Частотная диаграмма идеального ГСЧ
в случае проверки его на частотный тест

Также необходимо учитывать, что количество чисел, попавших в интервал (0; 0.5), должно быть примерно равно количеству чисел, попавших в интервал (0.5; 1).

3) Проверка по критерию «хи-квадрат»

Критерий «хи-квадрат» (χ²-критерий) — это один из самых известных статистических критериев; он является основным методом, используемым в сочетании с другими критериями. Критерий «хи-квадрат» был предложен в 1900 году Карлом Пирсоном. Его замечательная работа рассматривается как фундамент современной математической статистики.

Для нашего случая проверка по критерию «хи-квадрат» позволит узнать, насколько созданный нами реальный ГСЧ близок к эталону ГСЧ, то есть удовлетворяет ли он требованию равномерного распределения или нет.

Частотная диаграмма эталонного ГСЧ представлена на рис. 9.10. Так как закон распределения эталонного ГСЧ равномерный, то (теоретическая) вероятность p_i попадания чисел в i-ый интервал (всего этих интервалов k) равна p_i = 1/k. И, таким образом, в каждый из k интервалов попадет ровно по p_i · N чисел (N — общее количество сгенерированных чисел).

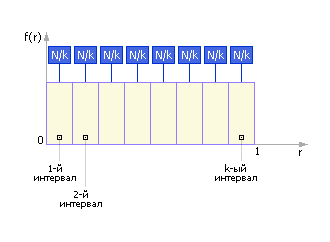
Рис. 9.10. Частотная диаграмма эталонного ГСЧ

Реальный ГСЧ будет выдавать числа, распределенные (причем, не обязательно равномерно!) по k интервалам и в каждый интервал попадет по n_i чисел (в сумме n₁ + n₂ + … + n_k = N). Как же нам определить, насколько испытываемый ГСЧ хорош и близок к эталонному? Вполне логично рассмотреть квадраты разностей между полученным количеством чисел n_i и «эталонным» p_i · N. Сложим их, и в результате получим:

χ²_эксп. = (n₁ – p₁ · N)² + (n₂ – p₂ · N)² + … + (n_k – p_k · N)².

Из этой формулы следует, что чем меньше разность в каждом из слагаемых (а значит, и чем меньше значение χ²_эксп.), тем сильнее закон распределения случайных чисел, генерируемых реальным ГСЧ, тяготеет к равномерному.

В предыдущем выражении каждому из слагаемых приписывается одинаковый вес (равный 1), что на самом деле может не соответствовать действительности; поэтому для статистики «хи-квадрат» необходимо провести нормировку каждого i-го слагаемого, поделив его на p_i · N:

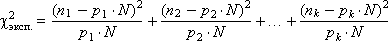
Наконец, запишем полученное выражение более компактно и упростим его:

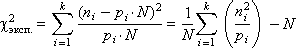
Мы получили значение критерия «хи-квадрат» для экспериментальных данных.

В табл. 9.2 приведены теоретические значения «хи-квадрат» (χ²_теор.), где ν = N – 1 — это число степеней свободы, p — это доверительная вероятность, задаваемая пользователем, который указывает, насколько ГСЧ должен удовлетворять требованиям равномерного распределения, или p — это вероятность того, что экспериментальное значение χ²_эксп. будет меньше табулированного (теоретического) χ²_теор. или равно ему.

Приемлемым считают p от 10% до 90%.

Если χ²_эксп. много больше χ²_теор. (то есть p — велико), то генератор не удовлетворяет требованию равномерного распределения, так как наблюдаемые значения n_i слишком далеко уходят от теоретических p_i · N и не могут рассматриваться как случайные. Другими словами, устанавливается такой большой доверительный интервал, что ограничения на числа становятся очень нежесткими, требования к числам — слабыми. При этом будет наблюдаться очень большая абсолютная погрешность.

Еще Д. Кнут в своей книге «Искусство программирования» заметил, что иметь χ²_эксп. маленьким тоже, в общем-то, нехорошо, хотя это и кажется, на первый взгляд, замечательно с точки зрения равномерности. Действительно, возьмите ряд чисел 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, … — они идеальны с точки зрения равномерности, и χ²_эксп. будет практически нулевым, но вряд ли вы их признаете случайными.

Если χ²_эксп. много меньше χ²_теор. (то есть p — мало), то генератор не удовлетворяет требованию случайного равномерного распределения, так как наблюдаемые значения n_i слишком близки к теоретическим p_i · N и не могут рассматриваться как случайные.

А вот если χ²_эксп. лежит в некотором диапазоне, между двумя значениями χ²_теор., которые соответствуют, например, p = 25% и p = 50%, то можно считать, что значения случайных чисел, порождаемые датчиком, вполне являются случайными.

При этом дополнительно надо иметь в виду, что все значения p_i · N должны быть достаточно большими, например больше 5 (выяснено эмпирическим путем). Только тогда (при достаточно большой статистической выборке) условия проведения эксперимента можно считать удовлетворительными.

Итак, процедура проверки имеет следующий вид.

1. Диапазон от 0 до 1 разбивается на k равных интервалов.
2. Запускается ГСЧ N раз (N должно быть велико, например, N/k > 5).
3. Определяется количество случайных чисел, попавших в каждый интервал: n_i, i = 1, …, k.
4. Вычисляется экспериментальное значение χ²_эксп. по следующей формуле:

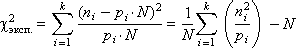
где p_i = 1/k — теоретическая вероятность попадания чисел в k-ый интервал.

1. Путем сравнения экспериментально полученного значения χ²_эксп. с теоретическим χ²_теор. (из табл. 22.2) делается вывод о пригодности генератора для использования. Для этого: а) входим в табл. 22.2 (строка = количество экспериментов – 1); б) сравниваем вычисленное χ²_эксп. с χ²_теор., встречающимися в строке. При этом возможно три случая.

Первый случай: χ²_эксп. много больше любого χ²_теор. в строке — гипотеза о случайности равномерного генератора не выполняется (разброс чисел слишком велик, чтобы быть случайным).

Второй случай: χ²_эксп. много меньше любого χ²_теор. в строке — гипотеза о случайности равномерного генератора не выполняется (разброс чисел слишком мал, чтобы быть случайным).

Третий случай: χ²_эксп. лежит между значениями χ²_теор. двух рядом стоящих столбцов — гипотеза о случайности равномерного генератора выполняется с вероятностью p (то есть в p случаях из 100).

Заметим, что чем ближе получается p к значению 50%, тем лучше.