Разложение матрицы в произведение простейших
Пусть 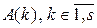 – некоторые матрицы. Введём следующее обозначение, предполагая при этом, что произведение в правой части существует,
– некоторые матрицы. Введём следующее обозначение, предполагая при этом, что произведение в правой части существует,
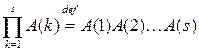 .
.
Предложение 1.5. Любую ненулевую матрицу из 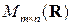 можно представить в виде произведения
можно представить в виде произведения
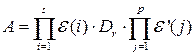 , (1.22)
, (1.22)
где 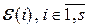 , – элементарные матрицы порядка
, – элементарные матрицы порядка 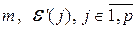 , – элементарные матрицы порядка
, – элементарные матрицы порядка 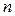 , и матрица
, и матрица 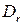 имеет вид (1.21).
имеет вид (1.21).
◄ В силу предложения 1.4 существует конечное число строчных и столбцовых элементарных преобразований, приводящих матрицу  к виду
к виду 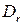 . Так как проведение одного строчного элементарного преобразования в матрице
. Так как проведение одного строчного элементарного преобразования в матрице  равносильно умножению этой матрицы слева на некоторую элементарную
равносильно умножению этой матрицы слева на некоторую элементарную 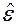 матрицу порядка
матрицу порядка 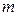 , а проведение в
, а проведение в  одного столбцового элементарного преобразования равносильно умножению матрицы
одного столбцового элементарного преобразования равносильно умножению матрицы  справа на некоторую элементарную матрицу
справа на некоторую элементарную матрицу 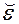 порядка
порядка 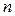 , получаем матричное равенство
, получаем матричное равенство
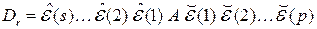 . (1.23)
. (1.23)
Матрицы 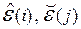 обратимы, а обратные им матрицы являются элементарными матрицами того же порядка. Поэтому, вводя обозначения
обратимы, а обратные им матрицы являются элементарными матрицами того же порядка. Поэтому, вводя обозначения
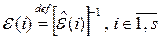 ,
,
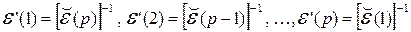 ,
,
и умножая обе части равенства (1.23) в соответствующем порядке на матрицы 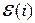 слева и на матрицы
слева и на матрицы 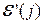 справа, получаем
справа, получаем
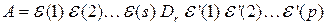 ,
,
т.е. равенство (1.22). ►
Пример 8. разложить матрицу
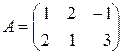
в произведение простейших.
◄ Элементарными преобразованиями приводим матрицу 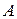 к виду
к виду 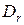 ,
,
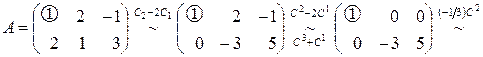
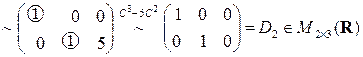 .
.
Проводим эквивалентную цепочку элементарных преобразований, умножая матрицу  слева на элементарную матрицу порядка 2, отвечающую элементарному преобразованию
слева на элементарную матрицу порядка 2, отвечающую элементарному преобразованию 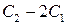 , и умножая её справа на элементарные матрицы порядка 3, отвечающие элементарным преобразованиям
, и умножая её справа на элементарные матрицы порядка 3, отвечающие элементарным преобразованиям 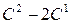 ,
, 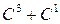 ,
, 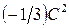 ,
, 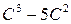 . В результате получаем, что
. В результате получаем, что
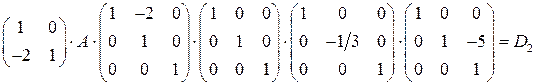 .
.
Определяя обратные элементарные матрицы (см. свойство 4 элементарных преобразований) и умножая на них в соответствующем порядке последнее равенство, получаем, что
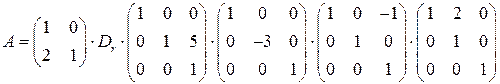 . ►
. ►
Следствием предложения 1.5 является критерий обратимости квадратной матрицы.
Предложение 1.6. (1-й критерий обратимости матрицы). Для того, чтобы матрица  была обратимой, необходимо и достаточно, чтобы она была представима в виде произведения элементарных матриц.
была обратимой, необходимо и достаточно, чтобы она была представима в виде произведения элементарных матриц.
◄ Достаточность. Элементарные матрицы обратимы, а произведение обратимых матриц есть матрица обратимая. Поэтому утверждение “матрица, представимая в виде произведения элементарных матриц, обратима” очевидно.
Необходимость. Пусть матрица  обратима. Покажем, что она представима в виде произведения элементарных матриц. Прежде всего заметим, что в силу предложения 1.5 справедливо равенство (1.22), где все матрицы, входящие в это равенство, квадратные и имеют одинаковый порядок, например,
обратима. Покажем, что она представима в виде произведения элементарных матриц. Прежде всего заметим, что в силу предложения 1.5 справедливо равенство (1.22), где все матрицы, входящие в это равенство, квадратные и имеют одинаковый порядок, например, 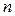 . Наше утверждение будет верно, если мы покажем, что
. Наше утверждение будет верно, если мы покажем, что 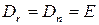 . В самом деле, матрицы
. В самом деле, матрицы
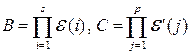
обратимы как произведение обратимых матриц. Поэтому обратимы матрицы 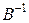 и
и 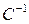 . Из равенства (1.22) получаем, что матрица
. Из равенства (1.22) получаем, что матрица
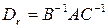
и является обратимой как произведение трёх обратимых матриц. Однако, матрица 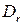 обратима в том и только том случае, когда
обратима в том и только том случае, когда 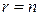 . Действительно,
. Действительно, 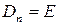 и поэтому обратима. Если же
и поэтому обратима. Если же 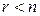 , то матрица
, то матрица 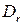 не может быть обратимой, так как последняя строка матрицы
не может быть обратимой, так как последняя строка матрицы 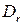 в этом случае нулевая и поэтому последняя строка произведения
в этом случае нулевая и поэтому последняя строка произведения 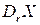 нулевая для любой матрицы
нулевая для любой матрицы 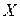 , т.е. равенство
, т.е. равенство 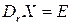 не может выполняться ни для каких матриц
не может выполняться ни для каких матриц 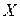 . В результате получаем, что матрица
. В результате получаем, что матрица  в данном случае имеет вид
в данном случае имеет вид
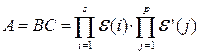 . ►
. ►
Пример 9. Выяснить, является ли следующая матрица обратимой
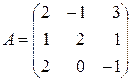
◄ Приводим матрицу  к виду
к виду 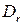 ,
,
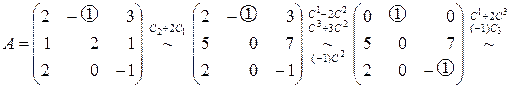
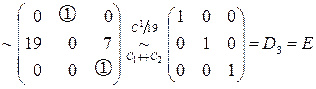 ,
,
т.е. матрица  обратима. Действуя дальше так же, как и в примере 6, можно представить матрицу
обратима. Действуя дальше так же, как и в примере 6, можно представить матрицу  в виде произведения элементарных матриц, а после этого найти обратную матрицу
в виде произведения элементарных матриц, а после этого найти обратную матрицу 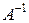 . Однако этот способ обращения матриц является слишком громоздким. Ниже в Гл.2 мы разберём более простой алгоритм отыскания обратной матрицы. ►
. Однако этот способ обращения матриц является слишком громоздким. Ниже в Гл.2 мы разберём более простой алгоритм отыскания обратной матрицы. ►
Вернёмся к предложению 1.2. Это предложение является следствием предложений 1.5 и 1.6. В самом деле, нам нужно показать, что любая ненулевая и необратимая матрица  из
из 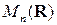 ,
, 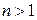 , является истинным делителем нуля.
, является истинным делителем нуля.
◄ Пусть 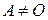 и
и 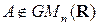 . В силу предложений 1.5 и 1.6
. В силу предложений 1.5 и 1.6 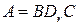 , где
, где 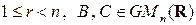 . Введём матрицы
. Введём матрицы
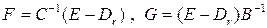
и отметим, что 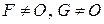 . Так как
. Так как 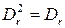 , то
, то
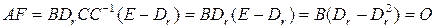 ,
,
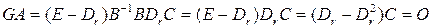 . ►
. ►
В заключение этого пункта предлагаем читателю самостоятельно доказать следующее усиление предложения 1.6.
Предложение 1.7. Пусть 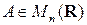 . Следующие утверждения равносильны:
. Следующие утверждения равносильны:
1) 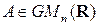 ;
;
2) 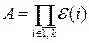 , где
, где 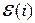 – элементарная матрица порядка
– элементарная матрица порядка 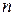 ;
;
3) 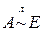 ;
;
4) 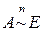 ;
;
5) 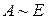 .
. 
Дата добавления: 2015-11-06; просмотров: 6088;
