Теория делимости квадратных матриц

Выше мы убедились, что арифметические операции над матрицами, прежде всего в части умножения, отличаются по своим свойствам от аналогичных операций над числами. Однако наиболее существенные отличия связаны с операцией деления.

Любое отличное от 0 действительное число 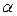имеет обратное число 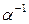, т.е.

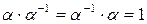, (1.11)

и поэтому любое действительное число 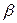можно разделить на любое ненулевое число ,

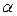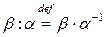
Теорию делимости для матриц будем строить, исходя из соотношений (1.11).

Матрица 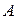называется обратимой, если существует такая матрица 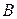, что

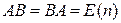. (1.12)

Если матрица 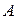обратима матрица 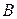называется её обратной матрицей и обозначается 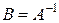. Из равенства (1.12) следует, что все входящие в них матрицы квадратные и имеют одинаковый порядок 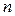. В связи с этим будем считать, что все матрицы, рассматриваемые в данном пункте, принадлежат множеству 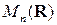, а единичную матрицу 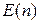будем обозначать для простоты 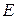. Множество всех квадратных обратимых действительных матриц порядка 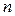в дальнейшем будем обозначать через .

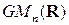Свойства обратимых матриц.

1) Если 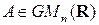, её обратная матрица 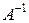единственна.

◄ Действительно, допустим, что наряду с равенствами (1.12) выполняются равенства

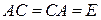. (1.13)

где 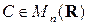. Умножая обе части равенства 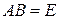на матрицу 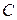слева, по свойству ассоциативности умножения матриц получаем, что

.

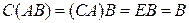С другой стороны,

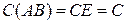, т.е. . ►

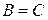2) Если 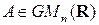, тогда 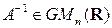, и .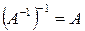

◄ Справедливость этого свойства вытекает из равенств (1.12). ►

3) Если 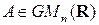, тогда 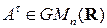, и

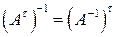. (1.14)

◄ Действительно, применяя операцию транспонирования к равенствам (1.12) и учитывая при этом, что 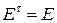, получаем, что

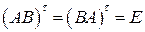
или

.

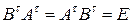Последнее равенство означает, что матрица 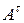обратима, и её обратная матрица имеет вид 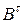, т.е. выполнено равенство (1.14). ►

4) Есл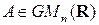и и 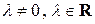, тогда матрица 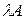обратима и

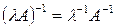. (1.15)

◄ Действительно, используя свойство 5) умножения матриц, получаем, что

,

.

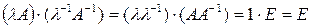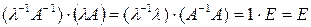Откуда следует обратимость матрицы 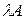и равенство (1.15). ►

5) Если 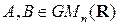, тогда 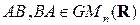и

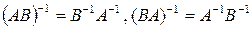(1.16)

◄ Докажем, например, обратимость матрицы ,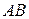

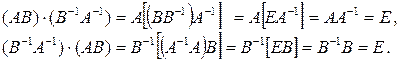
Откуда следует обратимость матрицы 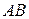и первое равенство (1.16). Обратимость матрицы 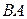и второе равенство (1.16) доказывается аналогично. ►

6) Если 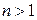, то во множестве 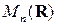всегда существует необратимые матрицы.

◄ Примером такой матрицы является матрица

.

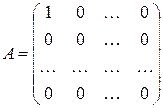Действительно, равенство 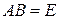не может выполняться ни для какой матрицы 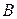из 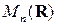, так как в произведении 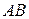последняя строка всегда нулевая и поэтому

.►

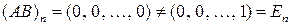Следующее утверждение по существу описывает все необратимые матрицы в .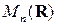

Предложение 1.1. Если матрица 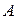является истинным делителем нуля, тогда она необратима.

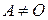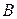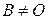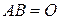◄ Пусть матрица и существует такая матрица , , что или 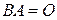. Тогда матрица 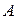не может быть обратимой. Действительно, если предположить существование такой матрицы 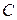, что

,

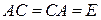тогда умножая обе части равенства 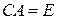на матрицу 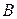справа (или обе части равенства 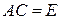на матрицу 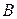слева), получаем, что

€

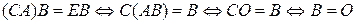и аналогично в случае . ►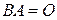

Справедливо и обратное утверждение.

Предложение 1.2. Если матрица 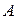отлична от нуль-матрицы и не является истинным делителем нуля, тогда она обратима.

Доказательство этого утверждения будет приведено позже в «Лекции V».

1.9. Основные типы алгебраических структур.

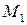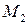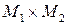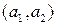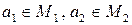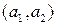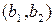Пусть и два произвольных непустых множества. Декартовым произведением этих множеств называется множество всевозможных упорядоченных пар вида , где . При этом две пары и , где 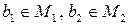, считаются равными, если 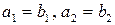. Если 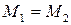, тогда множество 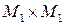называется декартовым квадратом множества .

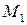Пусть 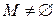. Внутренним законом композиции на множестве называется произвольное отображение декартова квадрата 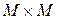во множество . Внутренний закон композиции на множестве каждой паре 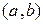элементов множества ставит в соответствие определенный элемент множества , который принято обозначать в виде сочетания трёх символов: элементов 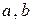и некоторого знака их соединяющего и одновременно позволяющего отличать друг от друга различные законы композиции, например,

,

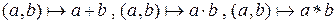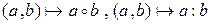и т.д.

Простейшими примерами внутренних законов композиции на множестве 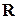являются арифметические операции сложения, вычитания и умножения действительных чисел, которые паре действительных чисел 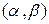ставят в соответствие их сумму, разность и произведение,

.

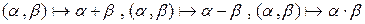Введенное выше поэлементное сложение матриц является внутренним законом композиции на множестве 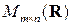, а умножение матриц – внутренним законом композиции на множестве .

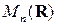Пусть 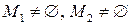. Внешним законом композиции на множестве 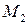над множеством 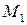называется произвольное отображение множества 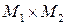во множество .

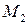Примером внешнего закона композиции на множестве матриц 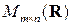над множеством действительных чисел 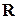является операция умножения матрицы на число,

.

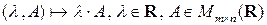Задание на некотором множестве одного или нескольких законов композиции, внутренних или (и) внешних, обладающих некоторыми стандартными свойствами, определяет на этом множестве различные алгебраические структуры (группы, поля, кольца, линейного пространства, алгебры и т.д.).

Если внутренний закон композиции на множестве , записываемый как умножение, обладает свойствами:

1) 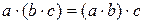(ассоциативность)

для любых 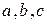из ;

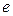2) в существует такой элемент , что

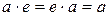(существование единицы)

для каждого 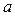из ;

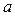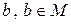3) для каждого элемента из найдется такой элемент , что

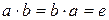(обратимость)

тогда говорят, что закон композиции определяет на структуру группы. Элемент 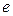называется при этом единицей группы, а элемент 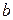из 3) – обратным к 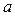элементом и обозначается .

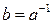Если наряду со свойствами 1) – 3) выполняется свойство

4) 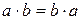(коммутативность)

для любых 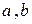из , такая группа называется абелевой. Свойства 1) – 3) называются аксиомами группы, а свойства 1) – 4) аксиомами абелевой группы. В абелевой группе закон композиции записывается обычно как сложение, в связи с чем её аксиомы принимают вид

1’) ;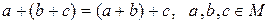

2’) в существует элемент 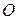такой, что

;

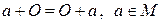3’) для любого 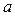из найдется элемент 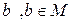, такой, что

;

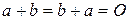4’) .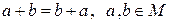

Элемент 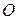называется нулем абелевой группы, а элемент 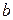из аксиомы 3’) – противоположным к элементу 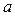и обозначается .

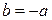Пример 3. а) Множество 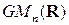является мультипликативной группой, т.е. операция умножения матриц определяет на этом множестве структуру группы.

◄ Действительно, из свойства 5) обратимых матриц следует, что умножение матриц является внутренним законом композиции на множестве 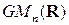. Аксиома группы 1) является следствием свойства 3) умножения матриц. Единичная матрица, очевидно, обратима, так как 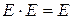, откуда следует аксиома группы 2), 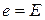. Аксиома группы 3) является следствием свойства 2) обратимых матриц. ►

б) Множество 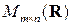является аддитивной абелевой группой, т.е. операция сложения матриц определяет на этом множестве структуру абелевой группы.

◄ Очевидно, что определенное выше поэлементное сложение матриц является внутренним законом композиции на множестве 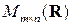, а аксиомы абелевой группы являются следствием свойств 1) – 4) сложения матриц. ►

Если на множестве определены два внутренних закона композиции, которые записываются как сложение и умножение и обладают свойствами:

1) сложение определяет на структуру абелевой группы;

2) ;

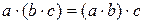3) 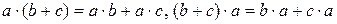для любых 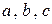из ,

тогда говорят, что на множестве задана структура кольца. Если при этом по умножению существует единица, это кольцо называется кольцом с единицей, а если операция умножения коммутативна, кольцо называется коммутативным.

Пример 4. а) Операции сложения и умножения чисел задают на множестве 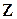структуру коммутативного кольца с единицей.

б) Операции сложения и умножения матриц задают на множестве 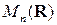, , 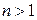структуру некоммутативного кольца с единицей.

Коммутативное кольцо с единицей, в котором все отличные от нуля элементы обратимы, называется полем. Важнейшими примерами полей являются поле рациональных чисел 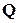и поле действительных чисел .

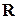Пусть задано непустое множество , элементы которого мы будем называть векторами, и поле 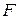с единицей 1. Если на множестве определены внутренний закон композиции, записываемый как сложение векторов,

,

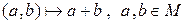и внешний закон композиции над полем 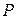, записываемый как умножение вектора на скаляр,

,

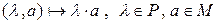и эти законы обладают свойствами:

1) сложение векторов определяет на структуру абелевой группы;

2) ,

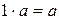3) ,

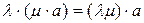4) ,

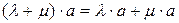5) ,

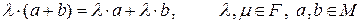тогда говорят, что на множестве задана структура линейного пространства над полем .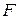

Пример 5. Операции сложения матриц и умножения матрицы на число задают на множестве 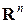структуру линейного пространства над полем 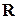или кратко структуру действительного линейного пространства.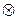

Непустое множество , на котором заданы два внутренних закона композиции (записываемых как сложение и умножение) и один внешний закон композиции над полем 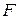(записываемый как умножение на число), называется алгеброй над полем 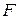, если:

1) сложение и умножение задают на структуру кольца,

2) сложение и умножение на число задают на структуру линейного пространства над полем ,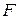

3) .

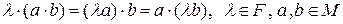Если умножение коммутативно, алгебра называется коммутативной, если умножение обладает единицей, алгебра называется алгеброй с единицей.

Пример 6. Из лекций I и II следует, что введённые там операции сложения и умножения матриц с операцией умножения матрицы на число задают на множестве 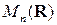при 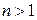структуру некоммутативной алгебры с единицей.