Элементарные преобразования над матрицами и элементарные
Матрицы
Элементарные преобразования над матрицами бывают только трёх типов:
1) перемена местами двух строк или столбцов; обозначения – 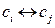 или
или 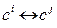 соответственно;
соответственно;
2) умножение строки или столбца на число, отличное от нуля; обозначения – 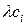 или
или 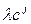 соответственно,
соответственно, 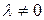 ;
;
3) добавление к какой-либо строке или столбцу другой строки или столбца, умноженных на произвольное число 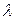 ; обозначения –
; обозначения – 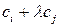 или
или 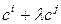 соответственно (элементарное преобразование этого типа называется трансвекцией).
соответственно (элементарное преобразование этого типа называется трансвекцией).
В результате применения к матрице  элементарного преобразования первого типа её строки
элементарного преобразования первого типа её строки 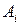 и
и 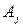 (или столбцы
(или столбцы 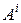 и
и 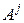 ) поменяются местами; во втором случае строка
) поменяются местами; во втором случае строка 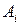 (или столбец
(или столбец 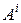 ) будет заменена на строку
) будет заменена на строку 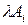 (или столбец
(или столбец 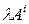 ); в последнем случае строка
); в последнем случае строка 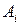 (или столбец
(или столбец 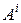 ) будет заменена на строку
) будет заменена на строку 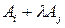 (или столбец
(или столбец 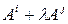 ), а строка
), а строка 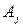 (столбец
(столбец 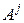 ) остается неизменной.
) остается неизменной.
Свойства элементарных преобразований.
1) Одно элементарное преобразование первого типа эквивалентно четырем элементарным преобразованиям второго и третьего типов.
◄ Пусть в матрице  нужно поменять местами, например, строки
нужно поменять местами, например, строки 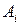 и
и 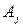 . Следующая цепочка элементарных преобразований второго и третьего типов приводит к результату
. Следующая цепочка элементарных преобразований второго и третьего типов приводит к результату
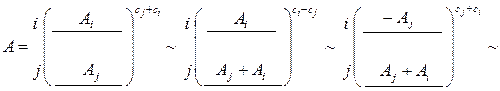
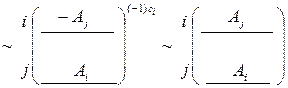 . ►
. ►
2) Элементарные преобразования обратимы, а обратные им преобразования являются элементарными преобразованиями того же самого типа, т.е. если матрица  получена из матрицы
получена из матрицы  с помощью элементарного преобразования, тогда матрица
с помощью элементарного преобразования, тогда матрица  может быть получена из матрицы
может быть получена из матрицы  с помощью элементарного преобразования того же самого типа.
с помощью элементарного преобразования того же самого типа.
◄ Используя для обозначения обратных элементарных преобразований символ ( )-1 непосредственной проверкой убеждаемся, что
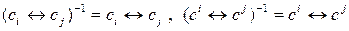 ,
,
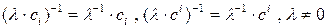 ,
,
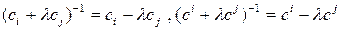 . ►
. ►
3) Квадратная матрица называется элементарной, если она получена из единичной матрицы с помощью одного элементарного преобразования. Несмотря на то, что имеется шесть видов элементарных преобразований, три строчных и три столбцовых, видов элементарных матриц всего три, так как одна и та же элементарная матрица может быть получена как с помощью строчного так и с помощью столбцового элементарных преобразований.
◄ Действительно, элементарные преобразования 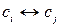 и
и 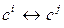 порождают одну и ту же элементарную матрицу
порождают одну и ту же элементарную матрицу
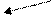
|
|
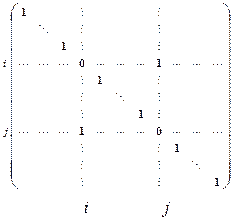 (1.17)
(1.17)
Элементарные преобразования 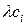 и
и 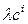 порождают одну и ту же элементарную матрицу
порождают одну и ту же элементарную матрицу
|

|
 (1.18)
(1.18)
Наконец, элементарные преобразования 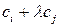 и
и 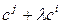 порождают одну и туже элементарную матрицу
порождают одну и туже элементарную матрицу
|
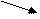
|
|
 (1.19)
(1.19)
4) элементарные матрицы обратимы, обратные им матрицы элементарны и порождаются элементарными преобразованиями, обратными исходным элементарным преобразованиям.
◄ Предлагаем читателю самостоятельно убедиться в том, что матрица вида (1.17) обратна самой себе, а матрицы
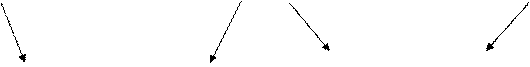
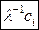
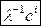
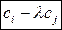
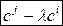
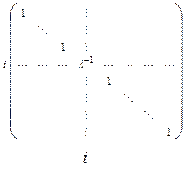

являются соответственно обратными матрицами матриц вида (1.18) и (1.19). ►
5) Пусть 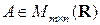 . Проведение в матрице
. Проведение в матрице  одного строчного (столбцового) элементарного преобразования равносильно умножению этой матрицы слева (справа) на элементарную матрицу порядка
одного строчного (столбцового) элементарного преобразования равносильно умножению этой матрицы слева (справа) на элементарную матрицу порядка 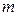 (порядка
(порядка 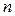 ), отвечающую этому элементарному преобразованию.
), отвечающую этому элементарному преобразованию.
◄ Ввиду свойства 1) элементарных преобразований в проверке нуждаются лишь элементарные преобразования второго и третьего типов. Предлагаем читателю показать самостоятельно, что умножение матрицы  вида (1.1) на матрицы вида (1.18) и (1.19) слева равносильно проведению в матрице
вида (1.1) на матрицы вида (1.18) и (1.19) слева равносильно проведению в матрице  элементарных преобразований соответственно
элементарных преобразований соответственно 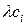 и
и 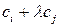 , а умножение на матрицы указанного вида справа равносильно проведению в ней элементарных преобразований соответственно
, а умножение на матрицы указанного вида справа равносильно проведению в ней элементарных преобразований соответственно 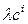 и
и 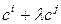 . ►
. ►
Лекция IV.
План
1.11 Эквивалентные матрицы
1.12* Отношение эквивалентности
Дата добавления: 2015-11-06; просмотров: 1317;
