Скалярное умножение арифметических векторов
Пусть
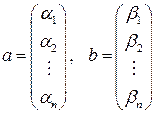
два арифметических вектора порядка 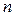 . Скалярным произведением этих векторов называется действительное число, которое обозначается
. Скалярным произведением этих векторов называется действительное число, которое обозначается  и находится по правилу
и находится по правилу
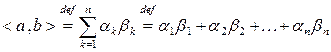 (1.7)
(1.7)
В дальнейшем будем также считать, что скалярное произведение двух векторов-строк порядка 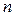 также вводится по формуле (1.7), т.е.
также вводится по формуле (1.7), т.е.
 .
.
Рассмотрим основные свойства скалярного умножения арифметических векторов.
1) Скалярное произведение симметрично, т.е. 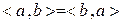 для любых
для любых 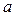 и
и 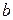 из
из  .
.
◄ Действительно,
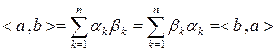
ввиду коммутативности операций умножения в 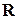 . ►
. ►
2) Скалярное произведение аддитивно по каждому из сомножителей, т.е.
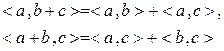
для любых 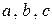 из
из  .
.
◄ Ввиду предыдущего свойства в доказательстве нуждается лишь одно из приведенных равенств. Покажем, например, справедливость первого равенства, где
Действительно,
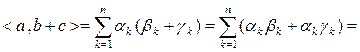
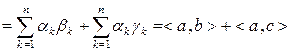 . ►
. ►
3) Скалярное произведение однородно по каждому из сомножителей, т.е.
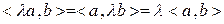
для любых действительных чисел  и любых векторов
и любых векторов 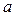 и
и 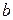 из
из  .
. 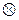
Арифметический вектор 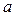 является линейной комбинацией векторов
является линейной комбинацией векторов 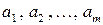 , если найдутся такие действительные числа
, если найдутся такие действительные числа 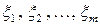 , что
, что
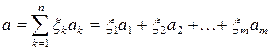 . (1.8)
. (1.8)
Из свойств 2) и 3) скалярного произведения следует, что если вектор 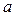 имеет вид (1.8), тогда
имеет вид (1.8), тогда

для любых векторов 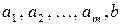 из
из  и любых действительных чисел
и любых действительных чисел 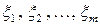 . Это свойство называется свойством линейности скалярного произведения по первому сомножителю. Аналогично имеет место свойство линейности скалярного произведения по второму сомножителю. В частности, если наряду с равенством (1.8) справедливо равенство
. Это свойство называется свойством линейности скалярного произведения по первому сомножителю. Аналогично имеет место свойство линейности скалярного произведения по второму сомножителю. В частности, если наряду с равенством (1.8) справедливо равенство
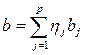 , где
, где  , тогда
, тогда
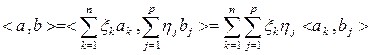 .
.
4) Скалярное произведение 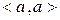 вектора
вектора 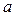 на себя называется скалярным квадратом вектора. Скалярный квадрат любого арифметического вектора есть число неотрицательное, т.е.
на себя называется скалярным квадратом вектора. Скалярный квадрат любого арифметического вектора есть число неотрицательное, т.е. 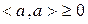 . Причём равенство
. Причём равенство 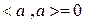 выполняется лишь для
выполняется лишь для 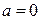 .
. 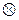
Умножение матриц
Пусть 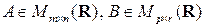 . Для того чтобы, существовало произведение
. Для того чтобы, существовало произведение 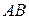 необходимо выполнение условия согласования
необходимо выполнение условия согласования 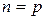 , т.е. число столбцов матрицы
, т.е. число столбцов матрицы 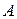 должно совпадать с числом строк матрицы
должно совпадать с числом строк матрицы 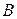 (или порядок строк матрицы
(или порядок строк матрицы 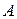 должен совпадать с порядком столбцов матрицы
должен совпадать с порядком столбцов матрицы 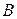 ). Если условие согласования выполнено, т.е.
). Если условие согласования выполнено, т.е.
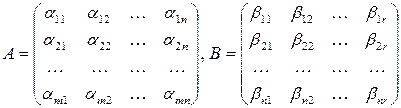
тогда произведение 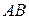 определено формулой
определено формулой
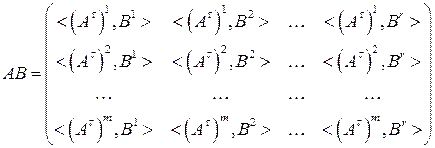 ,
,
т.е. если 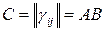 , тогда
, тогда
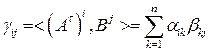
– элемент, стоящий в 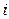 -ой строке и
-ой строке и 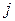 -ом столбце матрицы
-ом столбце матрицы 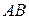 равен скалярному произведению
равен скалярному произведению 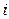 -ого столбца матрицы
-ого столбца матрицы 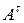 (или транспонированной
(или транспонированной 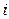 -ой строки матрицы
-ой строки матрицы 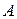 ) на
) на 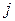 -ый столбец матрицы
-ый столбец матрицы 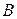 .
.
Пример 2. Пусть
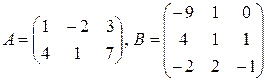
Так как  , то условие согласования для матрицы
, то условие согласования для матрицы 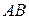 выполнено и
выполнено и
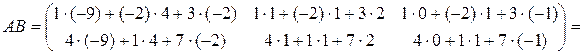
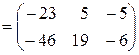 .
.
Отметим также, что произведение  в данном случае не существует, так как для него не выполнено условие согласования.
в данном случае не существует, так как для него не выполнено условие согласования.
Заметим, что существуют и другие способы умножения матриц, естественно, приводящие к другим результатам. Данный способ умножения матриц диктуется потребностями линейной алгебры и связан с произведением (композицией, суперпозицией) так называемых линейных преобразований. Всякое линейное преобразование определяется некоторой матрицей. Во второй части курса будет показано, что матрица произведения двух линейных преобразований равна произведению матриц этих преобразований в смысле введенного выше определения.
Рассмотрим основные свойства умножения матриц.
1) Если 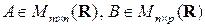 , тогда
, тогда 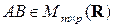 .
.
◄ Это свойство вытекает из определения произведения матриц. ►
2) Умножение матриц, вообще говоря, некоммутативно, т.е. 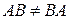 .
.
◄ Прежде всего заметим, что произведение 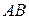 и
и  не всегда существуют одновременно, как это видно из примера 2. Если
не всегда существуют одновременно, как это видно из примера 2. Если 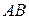 и
и  существуют одновременно, т.е.
существуют одновременно, т.е. 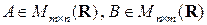 , тогда
, тогда  ,
, 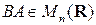 , т.е. при
, т.е. при  матрицы
матрицы 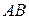 и
и  разного порядка и, следовательно, несравнимы. Но даже если
разного порядка и, следовательно, несравнимы. Но даже если  и, следовательно,
и, следовательно, 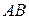 и
и  одного порядка, равенство
одного порядка, равенство 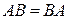 , вообще говоря, не выполняется. Например,
, вообще говоря, не выполняется. Например,

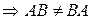 . ►
. ►
В то же время существуют матрицы 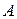 и
и 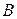 для которых
для которых 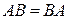 . Такие матрицы называются перестановочными. Например, матрицы
. Такие матрицы называются перестановочными. Например, матрицы

перестановочны, т.к.
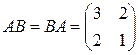 .
.
Более того, существуют квадратные матрицы порядка 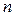 , которые перестановочны со всеми матрицами из
, которые перестановочны со всеми матрицами из 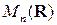 .
.
Примером такой матрицы во множестве 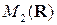 является матрица
является матрица
 ,
,
в чем предлагаем читателю убедиться самостоятельно.
3) Умножение матриц ассоциативно, т.е.
 . (1.9)
. (1.9)
Равенство (1.9) следует понимать так: если его левая (или правая) часть существует, тогда существует и правая (левая) часть и обе они совпадают.
Доказательство этого свойства содержится в учебнике [1], §13. 
4) Умножение матриц дистрибутивно относительно сложения, т.е.
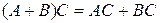 ,
, 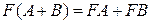
◄ Пусть  . Тогда
. Тогда
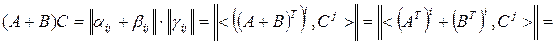
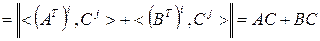 . ►
. ►
5) Произведение матриц однородно по каждому из сомножителей, т.е.
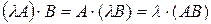 , где
, где 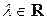 .
.
◄ Например,
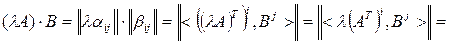
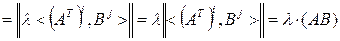 .
.
Равенство 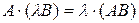 доказывается аналогично. ►
доказывается аналогично. ►
6) Реакция произведения матриц на операцию транспонирования выражается формулой
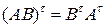 (1.10)
(1.10)
◄ Пусть 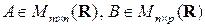 , тогда
, тогда 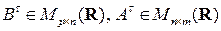 ,
,  , т.е. левая и правая части равенства (1.10) существуют и имеют одинаковые порядки. Далее
, т.е. левая и правая части равенства (1.10) существуют и имеют одинаковые порядки. Далее

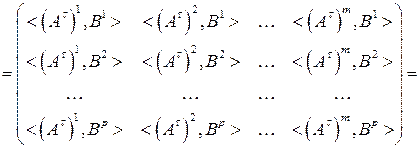
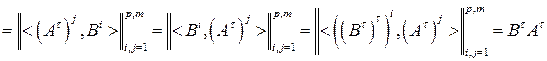 . ►
. ►
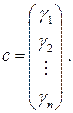
7) Рассмотрим множество квадратных матриц следующего вида:
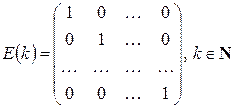 .
.
Матрица 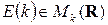 называется единичной матрицей порядка
называется единичной матрицей порядка 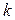 .
.
Если 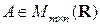 , тогда матрица
, тогда матрица 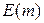 является её левой единицей, а матрица
является её левой единицей, а матрица 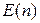 – правой единицей, т.е.
– правой единицей, т.е.
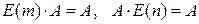 .
.
Если матрица 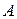 квадратная и имеет порядок
квадратная и имеет порядок 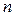 , тогда матрица
, тогда матрица 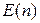 является её двусторонней (левой и правой) единицей, т.е.
является её двусторонней (левой и правой) единицей, т.е.
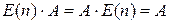 .
. 
8) Напомним, что для всех действительных чисел 
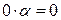 , т.е. ноль является делителем нуля. В то же время произведение
, т.е. ноль является делителем нуля. В то же время произведение 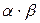 действительных чисел может равняться нулю лишь в том случае, когда по крайней мере одно из чисел
действительных чисел может равняться нулю лишь в том случае, когда по крайней мере одно из чисел  или
или 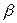 равно нулю. Иными словами, среди действительных чисел отсутствуют истинные (т.е. отличные от 0) делители нуля. В отличие от действительных чисел среди действительных матриц истинные делители
равно нулю. Иными словами, среди действительных чисел отсутствуют истинные (т.е. отличные от 0) делители нуля. В отличие от действительных чисел среди действительных матриц истинные делители  существуют, т.е. найдутся такие ненулевые матрицы
существуют, т.е. найдутся такие ненулевые матрицы 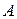 порядка
порядка 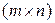 и
и 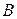 порядка
порядка 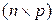 , что
, что 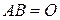 .
.
◄ В самом деле, матрицы
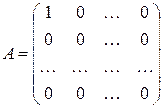 и
и 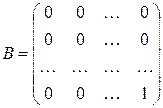 ,
,
соответственно порядков  и
и  , очевидно удовлетворяют нужному условию. В частности, если
, очевидно удовлетворяют нужному условию. В частности, если 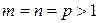 , то
, то 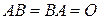 . ►
. ►
Лекция III.
План
1.8 Теория делимости квадратных матриц
1.9* Основные типы алгебраических структур
1.10 Элементарные преобразования над матрицами
и элементарные матрицы
Дата добавления: 2015-11-06; просмотров: 1860;
