Матрицы. Терминология
Алгебра матриц
В этой главе, прежде всего, строится матричное исчисление. На множестве матриц, определяемых как таблицы вещественных чисел, вводятся операции (сложения, умножения, умножения на число, транспонирования и обращения) и изучаются свойства этих операций. Выясняется, что наряду со свойствами операций, наследуемыми матрицами у вещественных чисел, у них появляются и новые свойства, которыми вещественные числа не обладают. Например, умножение матриц оказывается некоммутативным.
После этого обсуждается проблема разложения матрицы на простейшие. Оказывается, что любую матрицу единственным образом можно представить в виде суммы матриц, каждая из которых обладает только одним ненулевым элементом. Представление матрицы в виде произведения простейших является более сложным и нуждается в построении специального аппарата элементарных матриц, оправдывающего себя в последующих разделах курса.
В последней части первой главы изучаются простейшие матричные уравнения.
Матрицы. Терминология
Прямоугольная таблица действительных чисел
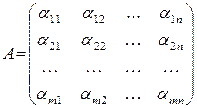 (1.1)
(1.1)
называется действительной матрицей. Числа 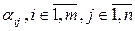 , образующие матрицу, называются её элементами. Здесь
, образующие матрицу, называются её элементами. Здесь 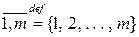 . Для обозначения матриц будем применять заглавные буквы латинского алфавита A, B, C, ..., X, Y, Z, а для обозначения их элементов – греческие буквы
. Для обозначения матриц будем применять заглавные буквы латинского алфавита A, B, C, ..., X, Y, Z, а для обозначения их элементов – греческие буквы 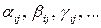 и т.д. с индексами
и т.д. с индексами 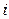 и
и 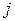 . При этом первый слева индекс (индекс
. При этом первый слева индекс (индекс 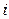 ) указывает номер строки, а второй индекс (индекс
) указывает номер строки, а второй индекс (индекс 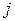 ) – на номер столбца матрицы, на пересечении которых расположен элемент
) – на номер столбца матрицы, на пересечении которых расположен элемент 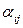 . Наряду с обозначением (1.1) в литературе часто встречаются сокращенные обозначения
. Наряду с обозначением (1.1) в литературе часто встречаются сокращенные обозначения
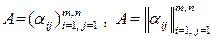
или просто 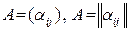 . Эти обозначения мы также будем использовать в дальнейшем.
. Эти обозначения мы также будем использовать в дальнейшем.
Введем специальные обозначения для строк и столбцов матрицы 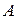 :
:
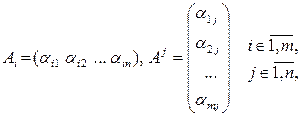
а множество всех действительных матриц с 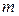 строками и
строками и 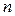 столбцами будем обозначать через
столбцами будем обозначать через 
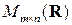 . Если
. Если 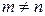 , матрица
, матрица 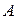 называется прямоугольной матрицей порядка
называется прямоугольной матрицей порядка 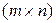 , а если
, а если  - квадратной матрицей порядка
- квадратной матрицей порядка 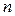 . Множество всех действительных квадратных матриц порядка
. Множество всех действительных квадратных матриц порядка 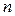 обозначается
обозначается 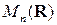 . Матрица
. Матрица 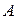 , имеющая только одну строку,
, имеющая только одну строку,
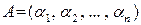 ,
,
называется матрицей-строкой порядка 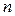 .
.
Матрица 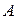 , имеющая только один столбец,
, имеющая только один столбец,
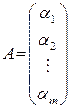 ,
,
называется матрицей-столбцом порядка 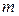 . Матрицы-строки и матрицы-столбцы называются также арифметическими векторами. Множество всех арифметических векторов (матриц-столбцов) порядка
. Матрицы-строки и матрицы-столбцы называются также арифметическими векторами. Множество всех арифметических векторов (матриц-столбцов) порядка 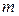 в дальнейшем будем обозначать через
в дальнейшем будем обозначать через 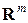 .
.
Элементы 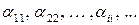 матрицы
матрицы 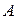 образуют её главную диагональ. Если все элементы матрицы
образуют её главную диагональ. Если все элементы матрицы 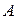 , не стоящие на её главной диагонали, равны нулю,
, не стоящие на её главной диагонали, равны нулю,
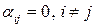 ,
,
матрица 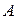 называется диагональной. Квадратная матрица
называется диагональной. Квадратная матрица 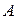 , у которой все элементы, стоящие выше (ниже) главной диагонали, равны нулю,
, у которой все элементы, стоящие выше (ниже) главной диагонали, равны нулю,
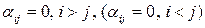
называется нижне-треугольной (верхне-треугольной) матрицей.
Понятие матрицы является одним из основных понятий курса алгебры. Элементами числовых матриц (целочисленных, рациональных, действительных, комплексных, булевых) являются числа (целые, рациональные, действительные, комплексные, булевы числа 0 и 1). В этом курсе мы будем иметь дело прежде всего с действительными матрицами. Тем не менее, обозначения 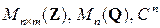 и т.д. имеют очевидный смысл. Наряду с числовыми матрицами в этом и других математических курсах встречаются более сложные типы матриц: полиномиальные, функциональные, блочные и т.д., то есть матрицы, элементами которых являются соответственно полиномы (многочлены), функции, блоки (матрицы одинакового порядка) и т.д. В связи с этим отметим, что все положения и свойства матриц, рассматриваемые в данном разделе, с надлежащими уточнениями справедливы и для других указанных выше типов матриц, характер же этих уточнений мы будем обсуждать всякий раз в соответствующем месте.
и т.д. имеют очевидный смысл. Наряду с числовыми матрицами в этом и других математических курсах встречаются более сложные типы матриц: полиномиальные, функциональные, блочные и т.д., то есть матрицы, элементами которых являются соответственно полиномы (многочлены), функции, блоки (матрицы одинакового порядка) и т.д. В связи с этим отметим, что все положения и свойства матриц, рассматриваемые в данном разделе, с надлежащими уточнениями справедливы и для других указанных выше типов матриц, характер же этих уточнений мы будем обсуждать всякий раз в соответствующем месте.
Принцип равенства
Две действительные матрицы 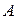 и
и 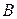 называются равными (записывается
называются равными (записывается 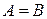 ), если они имеют одинаковые размеры, т.е. числа строк и столбцов у этих матриц совпадают, и на одинаковых местах в этих матрицах стоят одинаковые элементы.
), если они имеют одинаковые размеры, т.е. числа строк и столбцов у этих матриц совпадают, и на одинаковых местах в этих матрицах стоят одинаковые элементы.
Формализуем это определение: пусть
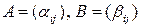 .
.
Тогда
 ,
,
где 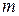 и
и 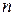 некоторые натуральные числа.
некоторые натуральные числа.
Пример 1. Выяснить, какие из следующих матриц равны
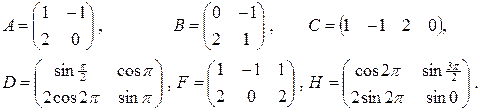
◄ Прежде всего заметим, что все шесть матриц порождены одними и теми же числами: 0, ±1, 2. Далее, сравнивать между собой можно только матрицы  и
и 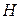 , являющиеся квадратными матрицами порядка 2, так как матрицы
, являющиеся квадратными матрицами порядка 2, так как матрицы 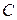 и
и 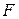 имеют соответственно размеры
имеют соответственно размеры 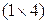 и
и 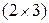 и, следовательно, не могут совпадать ни друг с другом, ни с остальными рассматриваемыми здесь матрицами. Матрица
и, следовательно, не могут совпадать ни друг с другом, ни с остальными рассматриваемыми здесь матрицами. Матрица 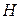 не совпадает ни с одной из матриц
не совпадает ни с одной из матриц  , так как в отличие от этих трёх матриц у
, так как в отличие от этих трёх матриц у 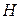 вторая строка целиком состоит из нулей. Далее
вторая строка целиком состоит из нулей. Далее 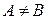 , так как на пересечении первой строки и первого столбца в этих матрицах стоят разные элементы: в
, так как на пересечении первой строки и первого столбца в этих матрицах стоят разные элементы: в 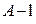 , а в
, а в 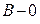 . Наконец, равенства
. Наконец, равенства  показывают, что
показывают, что 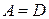 . ►
. ►
Дата добавления: 2015-11-06; просмотров: 1179;
