Отношение эквивалентности .

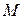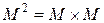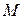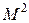Пусть – непустое множество произвольной природы и – его декартов квадрат. Бинарным отношением на множестве называется произвольное непустое подмножество в . бинарное отношение на множестве 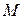можно определить указанием всех пар 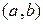, принадлежащих , говоря при этом, что элементы 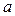и 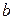из множества 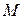находятся в отношении . Поскольку это не всегда удобно (например, если множество бесконечно), то высказывание “ 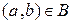” заменяется специальными высказываниями, зависящими от контекста, например,

.

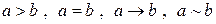которые читаются соответственно как “ 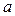больше 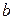”, “ 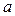равно 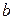”, “ 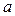влечёт 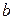”, “ 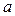эквивалентно ”

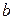Бинарное отношение на множестве 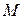называется отношением эквивалентности на множестве 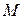, если оно удовлетворяет условиям:

1) 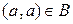для любого ,

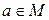2) если 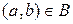, тогда ,

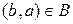3) есл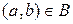и и 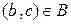, тогда .

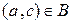Для отношения эквивалентности принято обозначение 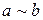. Условия 1)‑3), называемые аксиомами отношения эквивалентности, в этом обозначении выглядят так:

1’) 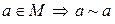, (рефлексивность)

2’) 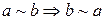, (симметричность)

3’) 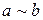и 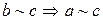. (транзитивность)

Введение на множестве 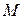какого-нибудь отношения эквивалентности приводит к разбиению множества на классы эквивалентности, то есть к представлению этого множества в виде объединения конечного или бесконечного числа попарно непересекающихся подмножеств эквивалентных между собой элементов. Множество классов эквивалентности при этом называется фактор-множеством множества 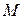по бинарному отношению и обозначается . 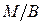Построение фактор-множества множества 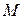по какому-нибудь отношению эквивалентности называется факторизацией множества 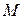. Задача факторизации множества является математической формализацией проблемы классификации объектов, с которой мы сталкиваемся не только в любой научной области, будь то физика (элементарные частицы), химия (таблица Менделеева), медицина (вирусология), лингвистика (части речи) или геология (классификация топов пород), но и в повседневной жизни (проблемы прописки, гражданства или деления Думы на фракции).

В алгебре матриц отношения “л‑эквивалентности”, “п‑эквивалентности” и “эквивалентности”, введенные в предыдущем пункте, являются отношениями эквивалентности на множестве 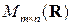. Наиболее важным из них является последнее отношение, которое приводит к построению фактор-множества, в одном классе эквивалентности которого содержатся те и только те матрицы, которые строчными и столбцовыми элементарными преобразованиями приводятся к матрице 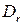вида (1.21) с данным 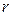. Нетрудно посчитать, что различных видов матриц 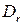всего 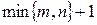. Это отношение эквивалентности в алгебре называется “одинаковый ранг” и подробно будет изучено во второй части нашего курса.

Предлагаем читателю самостоятельно рассмотреть фактор-множества 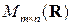по двум другим указанным выше отношениям эквивалентности при различных соотношениях между 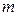и .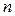

Лекция V.

План

1.13 Разложение матрицы в произведение простейших

1.14 Матричные уравнения