Матричные уравнения
Уравнение, называется матричным, если в качестве неизвестного оно содержит матрицу. Простейшие матричные уравнения имеют вид
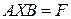 , (1.24)
, (1.24)
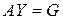 , (1.25)
, (1.25)
 , (1.26)
, (1.26)
где 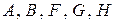 – известные матрицы, а
– известные матрицы, а 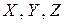 – неизвестные матрицы соответствующих размеров. В общем случае уравнения (1.24)-(1.26) эквивалентны некоторым системам линейных алгебраических уравнений (СЛАУ), но в том частном случае, когда матрицы
– неизвестные матрицы соответствующих размеров. В общем случае уравнения (1.24)-(1.26) эквивалентны некоторым системам линейных алгебраических уравнений (СЛАУ), но в том частном случае, когда матрицы  и
и  обратимы, теория этих уравнений проста. Прежде чем изложить её отметим, что числовая матрица
обратимы, теория этих уравнений проста. Прежде чем изложить её отметим, что числовая матрица 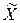 является решением уравнения (1.24), если при подстановке её в это уравнение вместо матрицы
является решением уравнения (1.24), если при подстановке её в это уравнение вместо матрицы 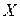 мы получаем верное матричное равенство (и аналогично для уравнений (1.25) и (1.26)).
мы получаем верное матричное равенство (и аналогично для уравнений (1.25) и (1.26)).
Предложение 1.8. Пусть матрицы  и
и  обратимы, тогда уравнения (1.24)-(1.26) разрешимы при любых правых частях
обратимы, тогда уравнения (1.24)-(1.26) разрешимы при любых правых частях 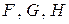 соответственно, а их единственные решения определяются по формулам
соответственно, а их единственные решения определяются по формулам
 , (
, ( 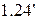 )
)
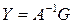 , (
, ( 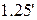 )
)
 , (
, ( 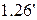 )
)
◄ Так как уравнения (1.25) и (1.26) являются частными случаями уравнения (1.24) ( 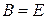 в первом случае и
в первом случае и 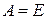 во втором случае), доказательство проведём лишь для уравнения (1.24). (Рассуждения в случае уравнений (1.25) и (1.26) предлагаем читателю провести самостоятельно.)
во втором случае), доказательство проведём лишь для уравнения (1.24). (Рассуждения в случае уравнений (1.25) и (1.26) предлагаем читателю провести самостоятельно.)
Пусть 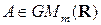 ,
, 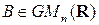 , тогда по необходимости матрицы
, тогда по необходимости матрицы 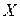 и
и 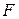 имеют размер
имеют размер 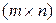 . Так как
. Так как  ,
, 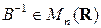 , то для любой матрицы
, то для любой матрицы 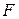 из
из 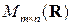 существует матрица
существует матрица 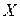 вида (
вида ( 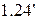 ). Подставляя её в уравнение (1.24), получаем
). Подставляя её в уравнение (1.24), получаем
 ,
,
т.е. матрица вида ( 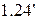 ) является решением уравнения (1.24). Тем самым показано, что решение уравнения (1.24) существует.
) является решением уравнения (1.24). Тем самым показано, что решение уравнения (1.24) существует.
Осталось показать его единственность. В самом деле, пусть 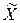 некоторое решение уравнения (1.24), тогда справедливо матричное равенство
некоторое решение уравнения (1.24), тогда справедливо матричное равенство
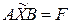 .
.
Умножая обе части слева на матрицу 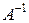 , а справа на матрицу
, а справа на матрицу 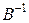 , получаем, что
, получаем, что
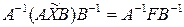
или
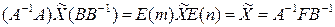 .
.
т.е. 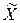 имеет вид (
имеет вид ( 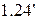 ). ►
). ►
Два матричных уравнения будем называть равносильными, если они имеют одинаковые решения. В частности, если у одного из равносильных уравнений решений нет, то их нет и у второго уравнения. В последнем случае мы предполагаем, что неизвестные матрицы, входящие в оба уравнения, имеют одинаковые размеры.
Предложение 1.9.Пусть 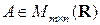 и
и  . Тогда уравнения
. Тогда уравнения
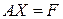 , (1.27)
, (1.27)
 (1.28)
(1.28)
равносильны для любых матриц 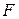 из
из 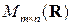 .
.
◄ Действительно, если 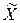 – решение уравнения (1.27), тогда
– решение уравнения (1.27), тогда 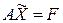 . Умножая обе части этого равенства слева на матрицу
. Умножая обе части этого равенства слева на матрицу 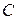 , получаем, что.
, получаем, что.
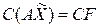 или
или  ,
,
т.е. 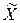 является решением уравнения (1.28). Наоборот, если
является решением уравнения (1.28). Наоборот, если 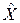 – решение уравнения (1.28), тогда
– решение уравнения (1.28), тогда
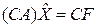 .
.
Но матрица 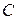 обратима. Умножая обе части последнего равенства слева на матрицу
обратима. Умножая обе части последнего равенства слева на матрицу 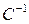 , получаем, что
, получаем, что
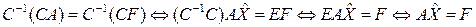 ,
,
т.е. 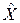 – решение уравнения (1.27). Если же у одного из уравнений (1.27) или (1.28) решений нет, тогда их нет и у второго уравнения, так как в противном случае, повторяя проведённые выше рассуждения, приходим к противоречию. ►
– решение уравнения (1.27). Если же у одного из уравнений (1.27) или (1.28) решений нет, тогда их нет и у второго уравнения, так как в противном случае, повторяя проведённые выше рассуждения, приходим к противоречию. ►
Упражнения
1. Выяснить, какие из следующих матриц равны
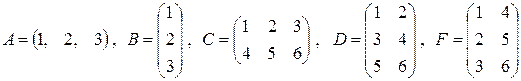 .
.
2. Написать матрицу, транспонированную данным:
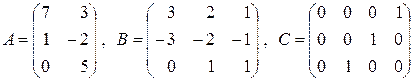 .
.
3. Если матрица 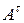 имеет вид
имеет вид
 ,
,
то каков вид матрицы  ?
?
4. Матрицы  и
и  имеют вид:
имеют вид:
а) 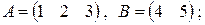 б)
б) 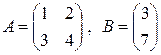 .
.
Каковы размеры матрицы 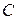 , если известно, что
, если известно, что 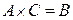 ?
?
5. Даны матрицы  и
и  . Найти матрицы
. Найти матрицы 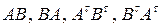 .
.
а)  ; б)
; б) 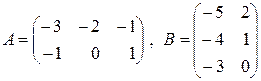 ;
;
в) 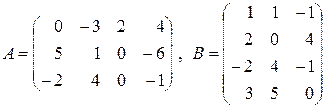 .
.
6. Найти произведение матриц 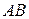 , если:
, если:
а) 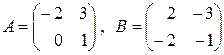 ; б)
; б) 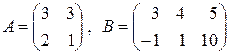 ;
;
в) 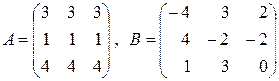 ; г)
; г) 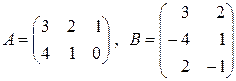
д) 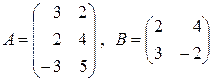 ; е)
; е) 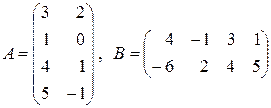 ;
;
ж) 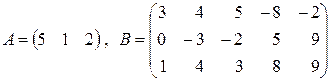 ;
;
з) 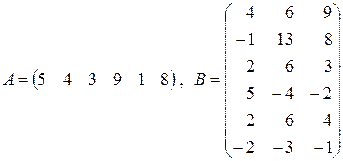 ;
;
и) 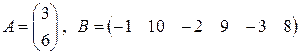 ; к)
; к) 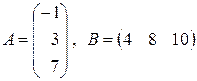 ;
;
л) 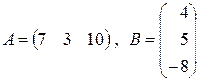 ; м)
; м) 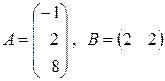 .
.
При вычислении сложных матричных выражений целесообразно продумать порядок действий, так как от этого зависит объём вычислений.
Пример 10. Найти матрицу 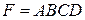 , если
, если
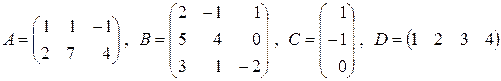 .
.
◄ Матрица 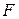 существует, так как порядки сомножителей согласованны
существует, так как порядки сомножителей согласованны
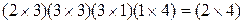 ,
,
и имеем порядок  . Благодаря свойству ассоциативности операции умножения матриц последовательность её вычисления может быть различной, например,
. Благодаря свойству ассоциативности операции умножения матриц последовательность её вычисления может быть различной, например,  или
или 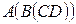 .
.
Напомним, что при вычислении произведения двух матриц используется скалярное умножение двух арифметических векторов порядка 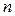 . Будем называть это скалярное умножение «простым», если
. Будем называть это скалярное умножение «простым», если  , и – «сложным», если
, и – «сложным», если 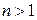 (сокращённо ПСУ и ССУ). Посчитаем количества ПСУ и ССУ, которые необходимо совершить, чтобы вычислить матрицу
(сокращённо ПСУ и ССУ). Посчитаем количества ПСУ и ССУ, которые необходимо совершить, чтобы вычислить матрицу 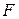 указанными выше способами.
указанными выше способами.
В первом случае последовательность вычислений такова:
1) 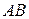 – 6 ССУ
– 6 ССУ
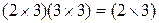
2) 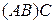 – 2 ССУ
– 2 ССУ
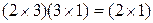
3)  – 8 ПСУ.
– 8 ПСУ.
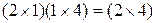
Всего: 8 ССУ и 8 ПСУ.
Во втором случае:
1)  – 12 ПСУ
– 12 ПСУ

2) 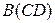 – 12 ССУ
– 12 ССУ
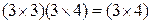
3) 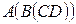 – 8 ССУ.
– 8 ССУ.
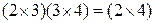
Всего: 20 ССУ и 12 ПСУ.
Преимущество первого способа над вторым очевидно. Но есть ещё один порядок умножения, позволяющий сократить объём вычислений. Именно, 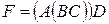 .
.
В самом деле,
1)  – 3 ССУ
– 3 ССУ
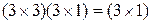
2) 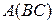 – 2 ССУ
– 2 ССУ
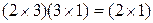
3) 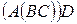 – 8 ПСУ.
– 8 ПСУ.
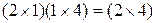
Всего: 5 ССУ и 8 ПСУ.
Анализ трёх рассмотренных способов вычисления матрицы  позволяет дать рекомендацию: при вычислении матричных произведений с числом сомножителей больше 2-х целесообразно начинать вычисление произведений с наименьшим числом столбцов у правого сомножителя, и заканчивать вычислением произведений с наибольшим числом столбцов у правого сомножителя. ►
позволяет дать рекомендацию: при вычислении матричных произведений с числом сомножителей больше 2-х целесообразно начинать вычисление произведений с наименьшим числом столбцов у правого сомножителя, и заканчивать вычислением произведений с наибольшим числом столбцов у правого сомножителя. ►
7. Найти произведение  , если:
, если:
а) 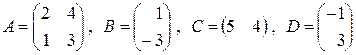 ;
;
б) 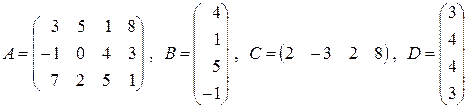 ;
;
в) 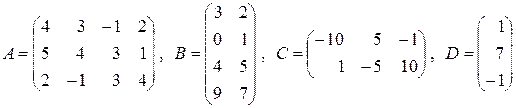 ;
;
г) 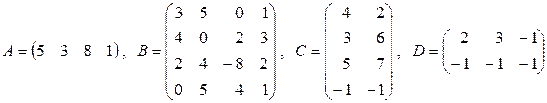 .
.
При вычислении матричных выражений вида 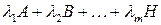 предварительно следует привести подобные члены, если это возможно.
предварительно следует привести подобные члены, если это возможно.
Пример 11. Найти матрицу
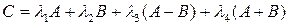 ,
,
если
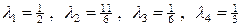 ,
,
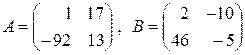 .
.
◄ Приводим подобные члены в исходном выражении для матрицы 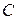 ,
,
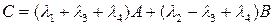 .
.
Так как
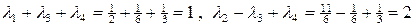 ,
,
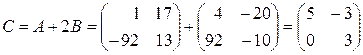 . ►
. ►
8. Найти матрицу 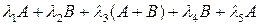 , если:
, если:
а) 
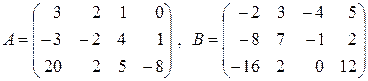 ;
;
б) 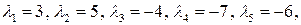
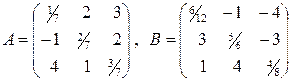 .
.
Часто сложное матричное выражение можно до его вычисления привести к более простому виду, используя свойства операций над матрицами.
Пример 12. Найти матрицу
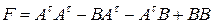 ,
,
если

◄ Заметив, что
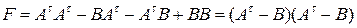 ,
,
где
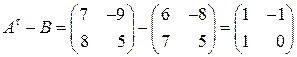 ,
,
получаем, что
 . ►
. ►
9. Найти матрицу 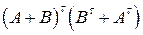 , если:
, если:
а) 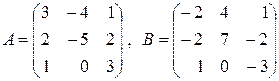 ;
;
б) 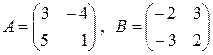 .
.
10. Найти матрицу 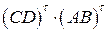 , если:
, если:
а)  ;
;
б) 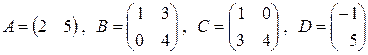 ;
;
в) 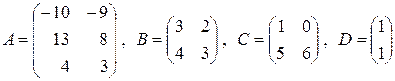 .
.
11. Найти матрицу  , если
, если
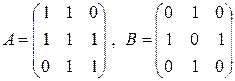 .
.
12. Найти матрицу 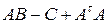 , если:
, если:
а)  ;
;
б) 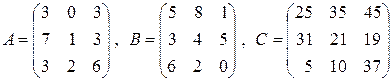 .
.
Введём обозначение для степени матрицы
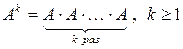 ,
,
И заметим, что ввиду некоммутативности операции умножения матриц
 .
.
Из условия согласования следует, что степень матрицы определена только для квадратных матриц, а степень произведения 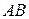 определена для матриц прямоугольного вида. При этом число строк матрицы
определена для матриц прямоугольного вида. При этом число строк матрицы 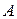 должно совпадать с числом столбцов матрицы
должно совпадать с числом столбцов матрицы 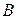 .
.
При вычислении степеней матриц и матричных выражений следует попытаться среди малых степеней 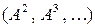 найти максимально простую матрицу с тем, чтобы использовать её для упрощения вычисления матрицы
найти максимально простую матрицу с тем, чтобы использовать её для упрощения вычисления матрицы 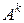 .
.
Пример 13. а) Найти матрицу
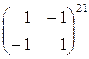 .
.
◄ Пусть 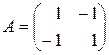 , тогда
, тогда 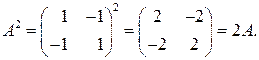
Поэтому
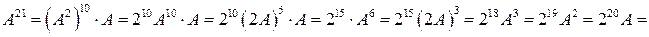
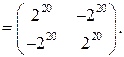 ►
►
б) Найти матрицу 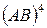 , где
, где
 .
.
◄ Рассмотрим матрицы 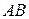 и
и 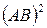 :
:
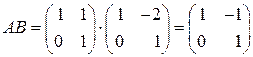 ,
,
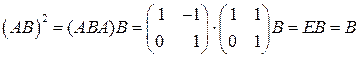 .
.
Но тогда
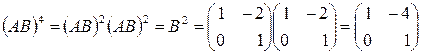 . ►
. ►
13. Вычислить значение матричного выражения:
а)  , если
, если 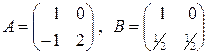 ;
;
б) 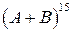 , если
, если 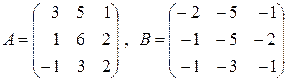 ;
;
в) 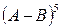 , если
, если
 ,
, 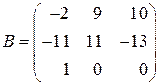 .
.
14. Вычислить  .
.
Пусть 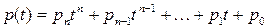 – многочлен,
– многочлен, 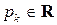 ,
, 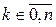 ,
, 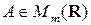 . Многочленом
. Многочленом 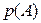 от матрицы
от матрицы 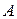 называется матричное выражение
называется матричное выражение
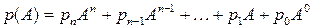 , где
, где 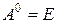 .
.
Пример 14. Найти значение 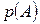 , если
, если
 .
.
◄ По определению
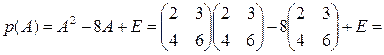
 . ►
. ►
15. Найти значение 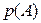 :
:
а) 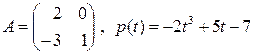 ;
;
б) 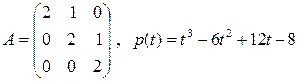 ;
;
в) 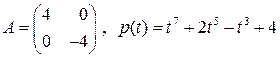 .
.
Аппарат элементарных матриц позволяет находить обратную матрицу, если исходная матрица обратима.
Пример 15. Разложить матрицу 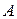 в произведение простейших. Выяснить, является ли матрица
в произведение простейших. Выяснить, является ли матрица 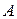 обратимой, и в случае её обратимости найти матрицу
обратимой, и в случае её обратимости найти матрицу 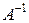 , если
, если
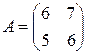 .
.
◄ Решение основано на предложении 1.6 (см. пример 9). Приводим элементарными преобразованиями матрицу 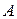 к виду
к виду 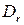 ,
,
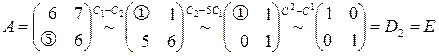 .
.
Матрица 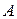 обратима и удовлетворяет соотношению
обратима и удовлетворяет соотношению
 .
.
Умножая полученное равенство справа на матрицу
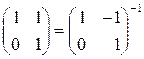 ,
,
получаем, что
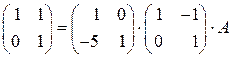 .
.
Теперь умножаем новое равенство на матрицу
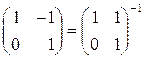
слева,
 .
.
Матрица 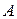 обратима и
обратима и  . Поэтому
. Поэтому
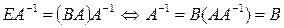 ).
).
Откуда следует что
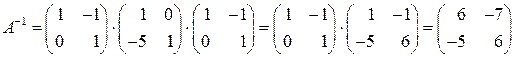 . ►
. ►
16. Указать элементарные матрицы, отвечающие следующим элементарным преобразованиям матрицы размера 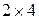 :
:
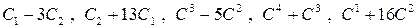 .
.
17. Каким элементарным преобразованиям матрицы размера 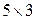 соответствуют элементарные матрицы:
соответствуют элементарные матрицы:
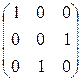 ,
, 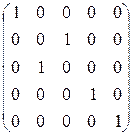 ,
,  ,
,
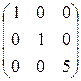 ,
,  ,
, 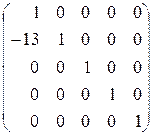 .
.
18. В матрице 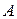 произвести элементарные преобразования умножением на соответствующие элементарные матрицы
произвести элементарные преобразования умножением на соответствующие элементарные матрицы 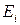 или
или 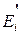 (
( 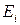 соответствуют строчным преобразованиям,
соответствуют строчным преобразованиям, 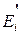 – столбцовым):
– столбцовым):
а) 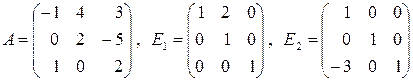 ,
,
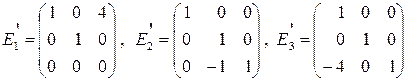 .
.
б) 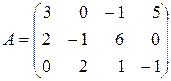 ,
,
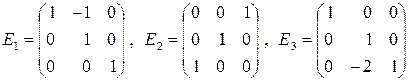 ,
,
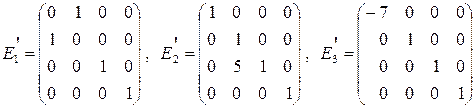 .
.
19. Элементарными преобразованиями привести матрицу к виду 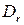 :
:
а) 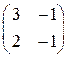 , б)
, б) 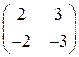 , в)
, в)  , г)
, г) 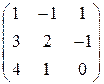 ,
,
д)  , е)
, е) 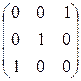 , ж)
, ж) 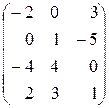 , з)
, з)  .
.
20. Матрицы из упражнения 19 разложить в произведение простейших.
21. Выяснить, является ли матрица 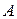 обратимой, и в случае её обратимости найти матрицу
обратимой, и в случае её обратимости найти матрицу 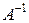 . Матрица
. Матрица 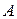 имеет вид:
имеет вид:
а) 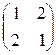 , б)
, б)  , в)
, в) 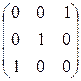 .
.
Замечание. В следующей главе, основываясь на данном методе обращения матриц, мы построим более эффективную вычислительную схему для нахождения обратной матрицы, связанную с методом Гаусса решения систем линейных алгебраических уравнений.
Дата добавления: 2015-11-06; просмотров: 2844;
