Векторно-матричные операции.
Все данные в системе MATLAB интерпретируются как массивы.
Массив – это упорядоченный набор однотипных данных (действительных и комплексных чисел, переменных, арифметических выражений). Каждый массив имеет имя. Массивы бывают одномерными, двумерными и многомерными. Доступ к конкретному элементу массива осуществляется путем указания его индекса (номера элемента в массиве).
Вектор в MATLAB – это одномерный массив, матрица – двумерный массив. По умолчанию программа предполагает, что каждая заданная переменная это вектор или матрица. Так, например, запись v=1 означает вектор, состоящий из единственного элемента = 1.
Способы задания векторов и матриц:
1.если значения элементов векторов являются арифметической прогрессией, такой вектор можно задать в виде:
имя = xn : dx : xk
где имя – имя, которое присваивается массиву; xn, xk – соответственно значения первого и последнего элементов массива, dx – шаг для формирования следующего элемента массива. Если параметр dx отсутствует, тогда шаг = 1 и вектор задается так:
имя = xn : xk
2.Поэлементный ввод. Для определения вектор-строки записывается имя массива, знак присваивания “=”, затем в квадратных скобках через пробел или запятую значения элементов массива, например, v=[1 2 3 4 5] или v=[1,2,3,4,5].
Элементы вектора-столбца вводятся через точку с запятой, например, v=[1;2;3;4;5].
Приобращении к элементу векторауказывается имя массива и порядковый номер элемента в круглых скобках, например v(1).
Ввод элементов матрицы осуществляется в квадратных скобках, при этом элементы строки отделяются друг от друга пробелом или запятой, а сами строки разделяются между собой точкой с запятой, например A=[1 2; 3 4]. Второй вариант задания той же матрицы
A=[1 2
3 4]
Обращение к элементу матрицы имеет вид: A(m,n), где m – номер строки элемента, n – номер столбца.
3. Путем объединения нескольких векторов. Результатом выполнения следующего фрагмента программы
>> a=[1 2 3];
>> b=[4 5 6];
>> c=[a b];
будет вектор с, содержащий элементы:
1 2 3 4 5 6
Результатом выполнения фрагмента программы
>> a=[1 2];
>> b=[3 4];
>> с=[a; b]
станет матрица с, имеющая вид
1 2
3 4
Формирование матриц и векторов определенного вида:
1. zeros(m,n) – прямоугольная матрица с нулевыми элементами, где m – число строк, n – число столбцов.
- zeros(m) – квадратная матрица с нулевыми элементами.
- ones(m,n) – прямоугольная матрица, состоящая из единиц;
- ones(m) – квадратная матрица, состоящая из единиц;
- eye(m,n) – прямоугольная матрица с 1 по главной диагонали, остальные элементы = 0.
- eye(m) – квадратная матрица из 1, расположенных по главной диагонали.
- diag(A) – извлечение главной диагонали матрицы A.
- diag(A,m) – извлечение любой диагонали матрицы A, m – номер извлекаемой диагонали (диагонали отсчитываются вверх и вниз от главной диагонали, у которой по умолчанию номер = 0).
Операции над векторами делятся на 2 типа:
1. Поэлементное преобразование (возможно только над векторами одинакового размера и типа). Признак поэлементной операции – точка перед знаком операции. В случае сложения или вычитания знак поэлементной операции ставить не нужно. Примеры: c=a.*b или d=k+p.
2. Векторные операции (сложение и вычитание векторов, транспонирование векторов, умножение на число, умножение вектора на вектор, скалярное и векторное произведение векторов). Примеры: b=x-y или z=x'.
Поясним, что для транспонирования применяется знак апостроф (’).
Умножение вектора на число выполняется с помощью обычного оператора умножения «*», причем умножать вектор на число можно и справа и слева.
Операции над матрицами:
- поэлементные операции (поэлементное умножение и деление матриц одинакового размера, поэлементное возведение в степень). Знаки, обозначающие соответствующие поэлементные операции эквиваленты векторным поэлементным операциям.
- матричные операции (сложение и вычитание матриц одинаковых размеров, умножение матрицы на число, умножение матрицы на матрицу; возведение матрицы в целую степень, транспонирование матрицы, участие в матричной операции обращенной матрицы). Перечисленные операции выполняются в MATLAB с помощью обычных арифметических операторов.
Некоторые функции для работы с векторами и матрицами.
· size(A) – определяется размер массива;
· length(a) – определяется количество элементов вектора;
· sort(a) – сортировка элементов вектора по возрастанию, где а – вектор. Если аргумент - матрица, тогда в результате функция упорядочивает каждый столбец матрицы отдельно;
· max(a) и min(a) – соответственно определение максимального (минимального) элемента вектора. Если аргумент этой функции – матрица, то результат – вектор-строка состоящая из максимальных (минимальных) элементов в соответствующих столбцах матрицы;
· dot(a,b) – скалярное произведение векторов a и b. Другой способ – матричное умножение транспонированного вектора a (строки) на вектор b (столбец). Пример: a’*b;
· eig(A) – возвращает вектор собственных значений матрицы А; [T,J]=eig(A) дает матрицу T, столбцы которой – собственные вектора матрицы A, и диагональную матрицу Jс собственными значениями матрицы A;
· inv(A) возвращает обратную матрицу к матрице A.
Пример 1.2. Вычислить скалярное произведение 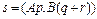 ,
,
где 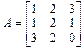 ;
; 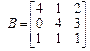 ;
;
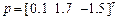 ;
; 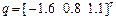 ;
; 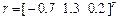 .
.
Найдем скалярное произведение 2 способами. Первый способ предполагает написание М-файла. Текст М-файла приведен ниже.
| A=[1 2 3;1 2 1;3 2 0]; B=[4 1 2; 0 4 3;1 1 1]; p=[.1;1.7;-1.5]; q=[-1.6;0.8;1.1]; r=[-0.7;1.3;0.2]; s=(A*p)'* B*(q+r) |
Второй способ предполагает использование режима командной строки:
>> A=[1 2 3;1 2 1;3 2 0];
>> B=[4 1 2; 0 4 3;1 1 1];
>> p=[.1; 1.7; -1.5];
>> q=[-1.6; 0.8; 1.1];
>> r=[-0.7; 1.3; 0.2];
>> s=dot(A*p,B*(q+r))
Получаемый результат:
s =
33.1700
Пример 1.3. Решить систему линейных алгебраических уравнений
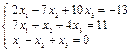
Текст соответствующего M-файла:
| A=[2 -7 10 7 1 4 1 -1 1] b=[-13; 11; 0] x=A\b |
Следует обратить внимание на то, что операция «деления» вектора b справа налево на матрицу А вызывает обращение матрицы А и умножение матрицы, обратной матрице А, на вектор b.
Получаемый результат:
A =
2 -7 10
7 1 4
1 -1 1
b =
-13
x =
-1
Пример 1.4. Определить собственные значения и собственные векторы матрицы
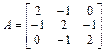
Текст соответствующего M-файла:
| A=[2 -1 0 -1 2 -1 0 -1 2] [T,J]=eig(A) |
Получаемый результат:
A =
2 -1 0
-1 2 -1
0 -1 2
T =
0.5000 -0.7071 -0.5000
0.7071 0.0000 0.7071
0.5000 0.7071 -0.5000
J =
0.5858 0 0
0 2.0000 0
0 0 3.4142
Дата добавления: 2015-09-28; просмотров: 1241;
