Понятие бинарной алгебраической операции.

Определение 1. Всякое отображение вида 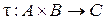называется бинарной операцией.

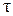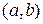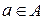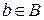Операция каждой упорядоченной паре , где , , ставит в соответствие единственный элемент 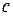из 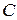, который обозначается через 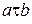. Запись 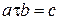означает, что элемент с является результатом операции 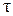, выполненной над элементами а и 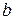– компонентами операции .

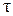Можно выделить несколько типов бинарных операций.

Определение 2. Отображение вида 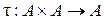называется алгебраической бинарной операцией на множестве 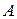или внутренней композицией.

Примерами таких операций будут сложение, умножение и вычитание на множестве 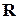, объединение и пересечение множеств, конъюнкция, дизъюнкция, импликация и эквиваленция высказываний и т.д.

Определение 3. Отображение вида 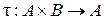называется внешней композицией.

Примеры: умножение вектора на число, умножение комплексного числа на действительное и т.д.

Рассматриваются также бинарные операции вида 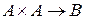. Примером такой операции является, например скалярное умножение векторов.

Определение 4.Отображения вида 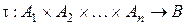называются n-арными операциями.

В частности, при 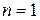операция называется унарной, при 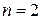– бинарной, а при 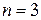– тернарной.

Таким образом, унарная операция каждому элементу из данного множества ставит в соответствие единственный элемент другого множества. Примерами унарных операций являются дополнение множеств, отрицание высказываний, навешивание кванторов, логарифмирование положительных чисел, возведение чисел в квадрат и т.д. Операция нахождения среднего арифметического трех действительных чисел является тернарной.

Определение 5.Отображения вида 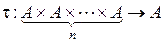называются n-арными алгебраическими операциями.

Мы будем рассматривать главным образом бинарные алгебраические операции. Очевидно, на множестве 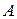определена бинарная алгебраическая операция 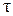, если любым двум элементам а и b множества 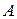, взятым в определенном порядке, ставится в соответствие единственный элемент того же множества 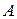, обозначаемый через .

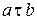При изучении алгебраических структур бинарные операции зачастую называют сложением или умножением и обозначают знаками + или 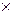(иногда, чтобы не путать с арифметическим сложением или умножением, знакам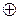и или 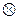); в первом случае говорят, что принята аддитивная терминология, во втором – мультипликативная терминология. При аддитивной терминологии результат операции называют суммой, а компоненты – слагаемыми; при мультипликативной терминологии результат операции называют произведением, а компоненты – сомножителями. Если нет оснований связывать операцию какой-нибудь терминологией, то будем обозначать ее значком 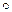. 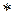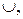В обычной математической практике для обозначения операций используют также символы ▪, •, , –, : , 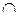, , 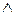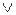и др.

В определении бинарной алгебраической операции имеется требование, чтобы результат операции, выполненной на любой паре элементов множества М, также принадлежал множеству М. Это так называемый постулат замкнутости множества относительно бинарной алгебраической операции (или замкнутости операции). С этой точки зрения нельзя считать бинарной алгебраической операцией, например, вычитание натуральных чисел или деление действительных чисел (деление на нуль невозможно).

Перейдем теперь к примерам бинарных алгебраических операций.

Пример 1.Обычное сложение и умножение на множествах N, Z, Q, R, Сявляются бинарными алгебраическими операциями.

Пример 2.Обычное вычитание является бинарной алгебраической операцией на множествах Z, Q, R, С.

Пример 3.Обычное деление на множествах 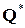, , 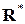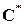является бинарной алгебраической операцией (здесь 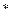означает, что из соответствующего множества удаляется число 0).

Пример 4.Для любых чисел 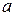и 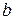из R положим

.

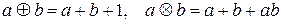Тогда 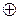, 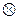– бинарные алгебраические операции на множестве R.

Пример 5.Для любых чисел 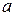и 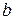из N положим

.

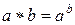Тогда 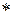– бинарная алгебраическая операция на множестве N.

В случае, когда множество М конечно, операцию 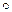на нем можно задать с помощью таблицы, называемой обычно таблицей Кэли (в честь выдающегося английского математика Артура Кэли (1821–1895)). Для этого элементы множества М располагают в верхней строке таблицы и в том же порядке – в левом столбце, а внутри таблицы помещают результаты операции над элементами из 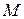. При этом элемент 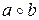располагают на пересечении строки, в которой стоит элемент а, и столбца, в котором стоит элемент b. Ввиду постулата замкнутости все клетки таблицы должны быть заполнены.

Пример 6. Пусть M = 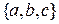. Зададим операцию 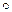на М с помощью табл. 1:

Таблица 1

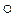
	a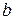
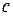
a	a	a	a
b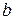

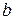
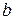
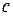
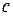
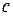
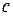
Эта таблица задает бинарную алгебраическую операцию 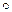на М по правилу x 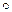y = x, т.е. результат операции 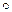для любой пары (x, y) элементов из М в данном примере равен левой компоненте.

С другой стороны, если операция задана на конечном множестве, то для наглядности ее можно проиллюстрировать с помощью таблицы Кэли.

Пример 7. Пусть M = 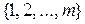, где m – натуральное число. Для любых элементов a и 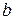из М положим 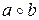= НОД 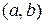. Тогда 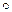– бинарная алгебраическая операция на М. Составим таблицу Кэли для m = 6.

Таблица 2

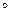
Пример 8.Пересечение 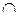и объединение 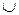являются бинарными алгебраическими операциями на булеане 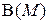подмножеств любого множества .

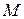Пример 9.Конъюнкция 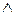и дизъюнкция 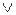являются бинарными алгебраической операциями на множестве высказываний.

Пример 10.Пересечение 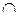, объединение 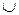и умножение 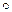являются бинарными алгебраическими операциями на множестве 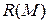всех бинарных отношения, заданных на множестве .

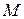2. Основные свойства алгебраических бинарных операций.Из школьногокурса математики хорошо известны такие свойства операций, как переместительный, сочетательный и распределительный законы для сложения и умножения чисел. Аналогичные свойства будем рассматривать для произвольных бинарных алгебраических операций. При этом используем более употребительные в математике термины, соответственно переместительный закон будем называть свойством коммутативности операции, сочетательный закон – свойством ассоциативности, распределительный закон – свойством дистрибутивности одной операции относительно другой.

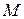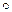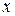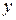Определение 5.Если во множестве с операцией для любых элементов и из 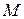справедливо равенство

,

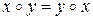то операция 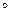называется коммутативной.

Заметим, что таблица Кэли для коммутативной операции симметрична относительно главной диагонали (см. табл. 2). Примерами коммутативных операций служат операции в примерах 1, 4, 7-10. Операции в примерах 2, 3, 5 и 6 не коммутативны.

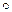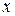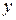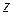Определение 6.Если во множестве М с операцией для любых элементов , и из 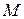справедливо равенство

,

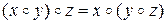то операция 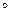называется ассоциативной.

Примерами ассоциативных операций служат операции в примерах 1, 4, 6, 7-10. Операции в примерах 2, 3, 5 не ассоциативны (проверка предоставляется читателю).

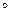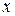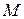Определение 7.Если во множестве М с операцией существует такой элемент е, что для любого элемента из справедливы равенства

,

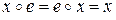то элемент е называется нейтральным относительно операции .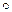

В случае аддитивной терминологии нейтральный элемент называют обычно нулем и обозначают символом 0; в случае мультипликативной терминологии нейтральный элемент называют обычно единицей и обозначают символом е или 1.

Нейтральным элементом относительно сложения во множествах Z, Q, R является число 0; относительно умножения во множествах N, Z, Q, R – число 1; относительно операции 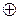из примера 4 – число –1, так как

.

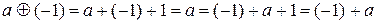относительно операции 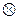из примера 4 – число 0, так как

.

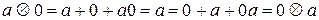Упражнение 1.Выяснить вопрос о существовании нейтрального элемента в остальных примерах.

Т е о р е м а 1.Если во множестве М с операцией 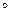существует нейтральный элемент e, то он единственный.

□ В самом деле, если 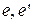– нейтральные элементы, то, с одной стороны, е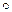 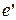= 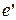, так как е – нейтральный элемент, а с другой стороны, е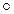 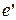= 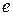, поскольку 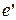– нейтральный элемент. В силу однозначности операции 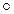отсюда получаем, что = .

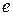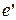Определение 8.Если во множестве М с операцией 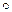и нейтральным элементом е, для элемента а из М существует такой элемент а 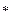, что справедливы равенства

,

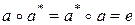то элемент 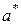называется симметричным к 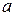относительно операции .

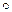В случае аддитивной терминологии симметричный к элементу а элемент 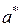называют противоположным к а и обозначают через 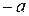; в случае мультипликативной терминологии – обратным к 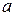и обозначают посредством .

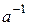Выясним, какие элементы обладают симметричными относительно операции 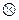из примера 4. Для этого возьмем произвольное действительное число а, рассмотрим уравнение 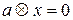и решим его относительно х. Согласно определению операции 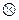имеем

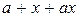= 0.

Отсюда 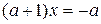и при 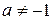имеем 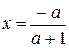. Таким образом, любой элемент, отличный от –1 (напомним, что это нуль относительно операции 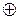из примера 4) имеет симметричный = .

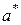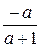Упражнение 2.Выяснить вопрос о существовании симметричного элемента в остальных примерах.

Т е о р е м а 2.Во множестве М с ассоциативной операцией 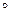и нейтральным элементом е каждый элемент обладает не более чем одним симметричным.

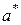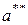□ Действительно, пусть и – симметричные по отношению к а из М элементы. Тогда, с одной стороны, имеем

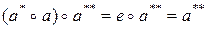, (1)

а с другой стороны,

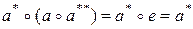. (2)

В силу ассоциативности операции 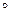левые части равенств (1) и (2) равны, а значит, равны и правые, т.е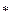. а = а .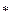

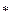Определение 9.Элемент 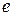множества М называется идемпотентом относительно операции 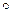, если е 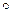е = е.

Понятно, что нейтральный элемент является идемпотентом (в частности, число 0 является идемпотентом относительно обычного сложения чисел, а число 1 – идемпотентом относительно обычного умножения чисел), но не всякий идемпотент является нейтральным (в примерах 6 и 7-10 все элементы являются идемпотентами).

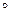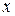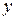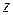Определение 10.Если во множестве М с операцией для любых элементов , и из 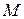справедлива импликация

,

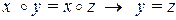то операция 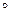называется сократимой слева; если в М справедлива импликация

,

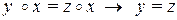то операция 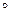называется сократимой справа. Если операция 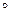сократима слева и сократима справа, то она называется просто сократимой.

Примерами сократимых операций являются обычноесложение на множествах N, Z, Q, R, C; обычное умножение во множествах N, 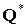, , 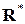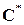. Операция, заданная табл. 1, сократима справа, но не сократима слева 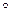(a b= a 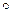c , но ).

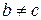Упражнение 3.Выяснить, какие из операций являются сократимыми в остальных примерах.

Определение 11.Если во множестве М с операцией 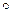для любых элементов a и 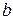из М однозначно разрешимы уравнения

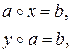
то операция 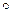называется обратимой.

Примерами обратимых операций являются обычное сложение во множествах Z, Q, R, C; обычное умножение во множествах Q*, R*, .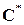

Упражнение 4.Выяснить, какие из операций являются обратимыми в остальных примерах.

Т е о р е м а 3. Если операция 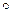является обратимой в М, то она обладает свойством сократимости.

□ Действительно, пусть 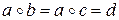. Тогда 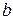и 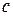– решения уравнения 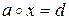. Поскольку операция 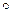обратима, это уравнение имеет единственное решение. Следовательно, 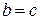. Таким образом, операция 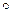сократима слева. Аналогично доказывается сократимость операция 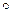справа.

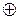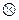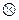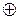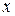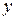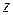Определение 12.Если на множестве М заданы две бинарные алгебраические операции и , то говорят, что операция дистрибутивна относительно операции , если для любых элементов , и из 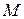справедливы равенства

,

.

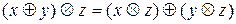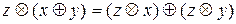Например, обычно умножение чисел дистрибутивно относительно сложения, операции пересечения и объединения множеств, как нам известно, дистрибутивны друг относительно друга, также как и операции конъюнкции и дизъюнкции.

Упражнение 5.Доказать, что в примере 4 операция 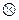дистрибутивна относительно операции .