Транспонированная матрица
Пусть матрица 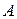 имеет вид (1.1). Тогда матрица
имеет вид (1.1). Тогда матрица
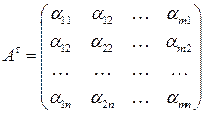
называется матрицей транспонированной к матрице 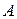 . Легко заметить, что, во-первых, матрицы
. Легко заметить, что, во-первых, матрицы 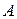 и
и 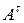 имеют одинаковые главные диагонали, а во-вторых, матрицу
имеют одинаковые главные диагонали, а во-вторых, матрицу 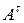 можно получить из матрицы
можно получить из матрицы 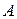 поворотом последней вокруг её главной диагонали на угол, равный
поворотом последней вокруг её главной диагонали на угол, равный 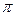 . В частности, если
. В частности, если
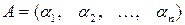 , тогда
, тогда 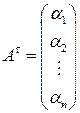 ,
,
и, наоборот, если
 , тогда
, тогда 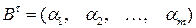 .
.
Отметим следующие очевидные свойства операции транспонирования матриц:
1) 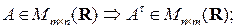 2)
2) 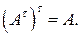
Если  , тогда матрица
, тогда матрица 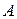 называется симметрической. Из свойства 1) следует, что симметрические матрицы всегда квадратные. Примером симметрической матрицы является матрица
называется симметрической. Из свойства 1) следует, что симметрические матрицы всегда квадратные. Примером симметрической матрицы является матрица
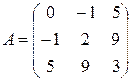 .
.
Сложение матриц
Операция сложения определена лишь для матриц одинакового размера. Именно, пусть 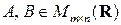 ,
,
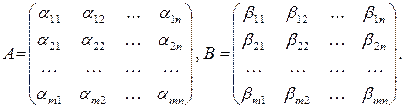
Суммой матриц  и
и 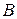 называется матрица
называется матрица
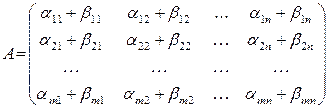 (1.2)
(1.2)
О сложении матриц говорят также, что оно осуществляется поэлементно. Как уже отмечалось выше, в процессе изучения алгебры матриц мы будем пользоваться упрощенными обозначениями 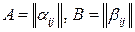 и т.д., не указывая всякий раз множества возможных значений индексов
и т.д., не указывая всякий раз множества возможных значений индексов 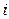 и
и 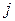 , поскольку эти значения будут ясны из контекста. Например, следующее определение суммы матриц эквивалентно вышеприведенному определению.
, поскольку эти значения будут ясны из контекста. Например, следующее определение суммы матриц эквивалентно вышеприведенному определению.
Пусть 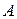 и
и 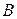 – действительные матрицы одного порядка, тогда
– действительные матрицы одного порядка, тогда
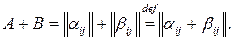 (1.3)
(1.3)
Знак 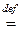 читается “равно по определению”, а отсутствие дополнительных указаний на возможные значения индексов
читается “равно по определению”, а отсутствие дополнительных указаний на возможные значения индексов 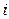 и
и 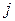 объясняется тем, что все матрицы, входящие в равенство (1.3), имеют одинаковый размер
объясняется тем, что все матрицы, входящие в равенство (1.3), имеют одинаковый размер  при некоторых натуральных значениях
при некоторых натуральных значениях 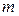 и
и 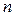 и, следовательно,
и, следовательно, 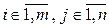 .
.
Операция сложения матриц обладает рядом свойств, роднящих её с операцией сложения действительных чисел.
1) Операция сложения матриц коммутативна, т.е. для любых 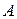 и
и 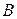 из
из 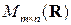
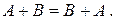
◄ Пусть 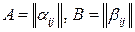 . Тогда
. Тогда
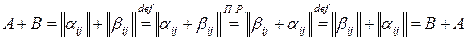 .
.
Здесь на первом и пятом шагах мы воспользовались обозначением суммы матриц, на втором и четвертом – определением суммы, а на третьем шаге – принципом равенства матриц. ►
2) Операция сложения матриц ассоциативна, т.е. для любых  и
и  из
из 
 .
. 
3) Среди всех матриц множества 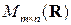 существует единственная матрица
существует единственная матрица  , обладающая свойством
, обладающая свойством
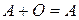 (1.4)
(1.4)
для любой матрицы 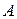 из
из 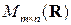 .
.
◄ Рассмотрим матрицу порядка  , все элементы которой равны 0. Ясно, что
, все элементы которой равны 0. Ясно, что 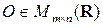 .
.
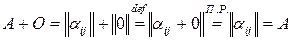
для любой матрицы 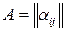 из
из 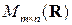 . Тем самым показано существование матрицы
. Тем самым показано существование матрицы  , обладающей нужным свойством. Для доказательства её единственности покажем, что любая матрица
, обладающей нужным свойством. Для доказательства её единственности покажем, что любая матрица 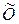 из
из 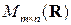 , удовлетворяющая равенству (1.4) для любых
, удовлетворяющая равенству (1.4) для любых 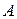 из
из 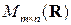 , совпадает с матрицей
, совпадает с матрицей  . Действительно, если матрица
. Действительно, если матрица 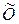 такая, как сказано выше, то одновременно выполняются равенства
такая, как сказано выше, то одновременно выполняются равенства
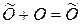 и
и 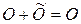 .
.
Используя свойство коммутативности сложения матриц, получаем, что 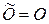 . ►
. ►
Матрица  называется нуль-матрицей, а свойство 3) – свойством существования и единственности нуль-матрицы.
называется нуль-матрицей, а свойство 3) – свойством существования и единственности нуль-матрицы.
4) Для любой матрицы 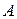 существует единственная матрица
существует единственная матрица 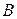 такая, что
такая, что
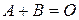 (1.5)
(1.5)
◄ Пусть 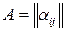 , тогда
, тогда 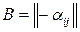 . Действительно,
. Действительно,
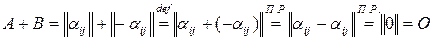 .
.
Тем самым доказано существование матрицы 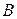 , удовлетворяющей равенству (1.5). Для доказательства её единственности предположим существование ещё одной матрицы
, удовлетворяющей равенству (1.5). Для доказательства её единственности предположим существование ещё одной матрицы 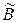 , удовлетворяющей равенству (1.5), т.е. равенству
, удовлетворяющей равенству (1.5), т.е. равенству
 (1.6)
(1.6)
Тогда
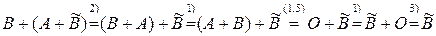 .
.
В то же время,
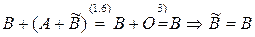 . ►
. ►
Матрица 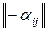 называется матрицей, противоположной матрице
называется матрицей, противоположной матрице 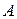 , и обозначается
, и обозначается 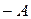 , а свойство 4) – свойством существования и единственности противоположной матрицы. С помощью противоположной матрицы вводится определение вычитания матриц, именно
, а свойство 4) – свойством существования и единственности противоположной матрицы. С помощью противоположной матрицы вводится определение вычитания матриц, именно
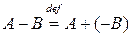 .
.
5) Операции сложения и транспонирования матриц связаны формулой
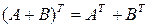
Дата добавления: 2015-11-06; просмотров: 772;
