Эмпирическая функция распределения

Одним из способов обработки вариационного ряда является построение эмпирической функции распределения. Напомним, что теоретической функцией распределения случайной величины Х называется функция F (x), определяющая для каждого значения х вероятность события {X<x}, то есть, вероятность события, заключающегося в том, что данная случайная величина Х принимает значения, не превосходящие х, то есть, F (x)=P(X<x).

Эмпирической функцией распределения случайной величины Х называется функция F_n(x), определяющая для каждого значения х частость, то есть относительную частоту, события {X<x}.

Для нахождения значений эмпирической функции распределения удобно записать её в виде относительной частоты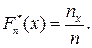

где n-объём выборки; n_x – число наблюдений Х, меньших х (х€R).

Очевидно, что удовлетворяет тем же условиям, что и теоретическая функция распределения.

При увеличении числа опытов (n) относительная частота события {X<x} приближается к вероятности P(X) этого события (теорема Бернулли). Эмпирическая функция распределения является оценкой вероятности события {X<x}, т.е. оценкой теоретической функции распределения F(x).

Имеет место

Теорема. Пусть F(x)- теоретическая функция распределения случайной величины Х, а - эмпирическая. Тогда для любого ɛ>0 справедливо равенство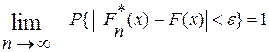

Пример 1.7. Построить эмпирическую функцию распределения по результатам примера 1.4. (о количестве неисправных соединений на АТС).

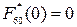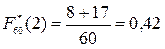Решение. В этом примере n=60. Имеем при х=0 (наблюдений меньше нуля нет); при 0≤х<1 и при 1≤x<2 и так д.алее.

Получим 0 при < 0,

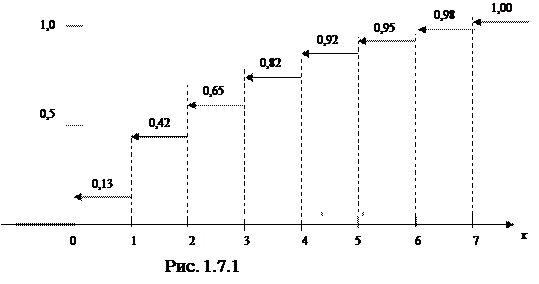
0,13 при 0≤ х <1

0,42 при 1≤ х <2

0,65 при 2≤ х <3

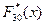= 0,82 при 3 ≤х <4

0,92 при 4≤ х < 5

0,95 при 5 ≤ х <6

0,98 при 6 ≤х <7

1,00 при x≥7

График эмпирической функции распределения будет иметь вид