Табличное представление выборки
|
|
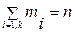 . Наблюдаемые значения хi называются вариантами. Если те значения х1, х2, …, хn, которые приняла случайная величина в n наблюдениях, записать не в порядке получения, а, например, в порядке их возрастания, то есть, ранжируем статистические данные, то получим упорядоченную выборку, называемую вариационным рядом.
. Наблюдаемые значения хi называются вариантами. Если те значения х1, х2, …, хn, которые приняла случайная величина в n наблюдениях, записать не в порядке получения, а, например, в порядке их возрастания, то есть, ранжируем статистические данные, то получим упорядоченную выборку, называемую вариационным рядом.
Выборка и вариационный ряд несут одну и ту же информацию, но с вариационным рядом легче работать в силу его упорядоченности.
Расстояние xmax- xmin между крайними членами вариационного ряда называется размахом вариационного ряда.
Для каждого полученного значения можно подсчитать, сколько раз оно встретилось в ряде наблюдений. Эти числа называются частотой варианта, или его весом.
Данные наблюдений, среди которых много повторяющихся, удобно изобразить в виде таблицы (табл. 1.1). Таблица 1.1
| Значения xi | x1 | x2 | . . . | xk |
| Частоты mi | m1 | m2 | . . . | mk |
Пример 1.4. На телефонной станции проводились наблюдения над числами Х неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1; …; 1; 1; 5. Расположив эти числа в порядке неубывания, получим следующий ряд: 0; 0; 0; 0; 0; 0; 0; 0; 1; 1; 1; … 5; 5; 7. Значения 0; 1; 2; …, 7, принятые случайной величиной в процессе наблюдений, являются вариантами.
Таблица 1.4.1
| Число неправильных соединений в мин, xi | |||||||||
| Частоты mi | ∑=60 |
xmax – xmin= 7-0=7 - размах вариационного ряда, mi – частота варианта.
Отношение mi/n, где mi – число повторений значения хi (его частота) в выборке объема n, называют относительной (эмпирической) частотой значения хi. Относительная частота – характеристика более универсальная, чем просто частоты, так как позволяет сравнивать выборки разного объема.
Построим по выборке таблицу из двух строк, в верхней строке которой указаны в порядке возрастания наблюдаемые значения хi, а в нижней - соответствующие им относительные частоты.
Эта таблица, содержащая значения наблюдаемой величины хi и относительной (эмпирической) частоты mi/n этой величины, называется таблицей статистического распределения выборки (табл. 1.2).
Таблица 1.2
| Значения xi | x1 | x2 | . . . | xk |
| Относительные частоты, mi/n | m1/n | m2/n | . . . | mk/n |
Пример 1.5. Для примера 1.4 таблица статистического распределения выборки имеет вид:
Таблица 1.5.1
| Число неправильных соединений в мин, xi | |||||||||
| Относительные частоты, mi/n | 8/60 (0,13) | 17/60 (0,28) | 14/60 (0,23) | 10/60 (0,17) | 6/60 (0,10) | 2/60 (0,03) | 2/60 (0,03) | 1/60 (0,02) | ∑=1 |
Если изучается величина, имеющая непрерывное распределение вероятностей, то возможные значения заполняют целый интервал или всю числовую ось. В этом случае, скорее всего, вариационный ряд не будет содержать повторяющихся значений. То же самое может иметь место, если наблюдение производится над дискретной случайной величиной, число возможных значений которой очень велико.
Для выборки, в которой нет повторяющихся значений, таблица статистического распределения выборки будет иметь вид
Таблица 1.3
| Значения xi | x1 | x2 | . . . | xn |
| Относительные частоты mi/n | 1/n | 1/n | . . . | 1/n |
Такая таблица при большом числе наблюдений не содержит полезной информации.
В случае, когда вариационный ряд содержит много разных значений наблюдаемой величины, прибегают к группировке данных.
Группировка состоит в том, что область на оси х, куда попали значения х1, …, хk, разбивают на частичные интервалы I1, …, Ik (k<m) и подсчитывают частоту попадания значений случайной величины в каждый интервал.
Обычно группировку стараются провести таким образом, чтобы значения, различия которых для практики незначимо, попали в один и тот же интервал, а те значения, различия которых значимы, попали в разные интервалы. Число частичных интервалов k следует брать не очень большим, чтобы после группировки ряд не был громоздким, и не очень малым, чтобы не потерять особенности распределения признака.
Для определения величины частичного интервала (h) можно использовать формулу Стерджеса:
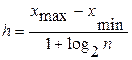
где хmin , xmax – наименьшее и наибольшее значения признака. Рекомендуемое число частичных интервалов брать равным k = 1+log2n ≈ 1 + 3,322 lg n. Обычно берут от 6 до 15 частичных интервалов, однако фактическое число частичных интервалов и, соответственно, размер частичного интервала определяются условиями конкретной задачи. За начало первого интервала рекомендуется брать величину xнач = хmin– h/2.
Вариационный ряд, представленный соответствующей таблицей, построенной с помощью процедуры группировки, называют интервальным статистическим рядом (в отличие от дискретного ряда, полученного по выборке из дискретного распределения вероятностей).
В первую строку таблицы статистического распределения группировки записывают частичные промежутки [x0, x1), [x1, x2), …, [xk-1, xk), которые обычно берут одинаковыми по длине h= x1- x0 = x2 - x1= …
Во вторую строку таблицы вписывают количество наблюдений mi, (i=1,k), попавших в каждый интервал.
Числа mi, показывающие, сколько раз встречаются варианты xi в ряде наблюдений, называются частотами, а отношение их к объёму выборки - частостями или относительными частотами p*i = mi/n.
В третью строку таблицы вписывают значения частостей (относительных частот) p*i
Пример 1.6(Письменный Д.Т., стр. 217). Измерили рост (с точностью до 1 см.) 30 наугад отобранных студентов. Результаты измерений таковы:
178, 160, 154, 183, 155, 153, 167, 186, 163, 155, 157, 175,170, 166, 159,
173, 182, 167, 171, 169, 179, 165, 156, 192, 158, 171, 175, 173, 164, 172.
Построить интервальный статистический ряд.
Решение. Для удобства проранжируем полученные данные, то есть составим упорядоченную выборку – вариационный ряд:
153, 154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167,
169, 170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 182, 183, 186, 192.
Отметим, что Х – рост студента – непрерывная случайная величина. При более точном измерении роста значения случайной величины Х обычно не повторяются (вероятность наличия на Земле двух человек, рост которых равен, скажем 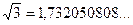 метров, равна нулю!).
метров, равна нулю!).
Как видим, хmin = 153, xmax = 192/ По формуле Стерджеса, при n=30, находим длину частичного интервала
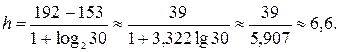
Примем h=6. Тогда 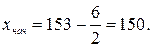 Исходные данные разбиваем на 7 (
Исходные данные разбиваем на 7 ( 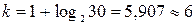 ) интервалов с шагом 6 см: [150, 156), [156, 162), [162, 168), [168, 174), [174, 180), [180, 186), [186, 192).
) интервалов с шагом 6 см: [150, 156), [156, 162), [162, 168), [168, 174), [174, 180), [180, 186), [186, 192).
Подсчитав число студентов (mi), попавших в каждый из полученных промежутков и их относительные значения (p*i), получим интервальный статистический ряд:
| [150, 156) | [156, 162) | [162, 168) | [168, 174) | [174, 180) | [180, 186) | [186, 192) | ||
| Частота | |||||||||
| Относительная частота | 4/30 (0,13) | 5/30 (0,17) | 6/30 (0,20) | 7/30 (0,23) | 4/30 (0,13) | 2/30 (0,07) | 2/30 (0,07) |
Дата добавления: 2015-11-06; просмотров: 3253;
