Выборка без расчленения генеральной совокупности.

Простой случайный отбор – это отбор, при котором объекты выборки случайным образом по одному извлекаются из всей генеральной совокупности. Осуществить случайный отбор можно различными способами.

Например, все объекты генеральной совокупности нумеруют, номера записывают на отдельные карточки, карточки перемешивают и выбирают наугад. Объект, номер которого совпал с номером на карточке, считается попавшим в выборку. Операцию повторяют до тех пор, пока не наберется нужный объем выборки. При этом:

- если случайно отобранная карточка возвращается обратно в общую совокупность, и, следовательно, раз отобранный в выборку объект может быть отобран повторно, то имеет место выборка повторная или выборка с возвратом;

- если отобранная карточка и, следовательно, отобранный в выборку объект назад не возвращается, то осуществляется выборка бесповторная или выборка без возврата.

При большом объеме генеральной совокупности данная процедура оказывается весьма трудоемкой. В этом случае вместо перемешивания карточек, можно использовать таблицы «случайных чисел». Их можно найти в большинстве книг по статистике. Открывают любую страницу таблицы и выписывают подряд n чисел. Объекты, номера которых совпадает с выписанными случайными числами, попадают в выборку. Таких таблиц сейчас издано много; разработаны программы для ЭВМ – генераторы случайных чисел.

Следует заметить, что если в выборке с возвратом испытания независимы, то в выборке без возврата испытания уже зависимы. Для демонстрации разницы между этими схемами рассмотрим простейший пример.

Пример 1.3. В урне n белых и m черных шаров. Наугад вынимаем два шара. Пусть событие А₁ –{первый шар белый}, А₂ – {второй шар тоже белый}.

а) выборка с возвратом:

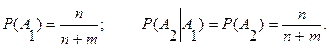
б) выборка без возврата:

Для того, чтобы найти вероятность р(А₂), определим событие В₁ – {первый вынутый шар – черный} и воспользуемся формулой полной вероятности:

р(А₂) = р(А₁)∙р(А₂/А₁)+р(В₁)∙р(А₂/В₁) =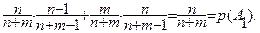

Заметим, что в данном случае р(А₂/А₁) =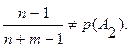

Таким образом, для выборки с возвратом вероятность во втором испытании вытащить белый шар такая же, как и в первом испытании: условная вероятность совпадает с безусловной, следовательно, испытания независимы. Для выборки без возврата вероятность во втором испытании вытащить белый шар такая же, как и в первом испытании, но независимости испытаний уже нет. Легко видеть, что если n и m велики, то зависимость испытаний является слабой. Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается.