Графическое представление выборки.

Для наглядного представления статистического распределения пользуются графическим изображением вариационных рядов: полигон, гистограмма, кумулята.

а) в случае дискретного распределения случайной величины строят полигоны, которые бывают двух видов: полигоны частот и полигоны относительных частот.

Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами (x₁, m₁), (x₂, m₂), …, (x_k, m_k).

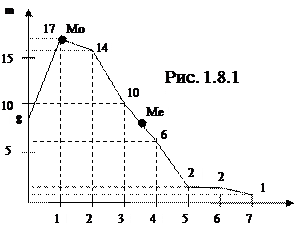
Для построения полигона частот на оси абсцисс откладывают отдельные значения признака х_i. Из «принимаемых» значений х_i проводят перпендикуляры, длины которых пропорциональны частотам m_i, затем концы соседних перпендикуляров соединяют отрезками прямых. Это полигон для дискретных вариационных рядов.

Пример 1.8.Полигон частот числа неправильных соединений в минуту на телефонной станции, построенный по таблице 1.4.1 (к примеру 1.4), приведен на рис. 1.8.1.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки с координатами (x₁, w₁), (x₂, w₂), …, (x_k, w_k), где w_i =m_i /n – относительные частоты случайной величины.

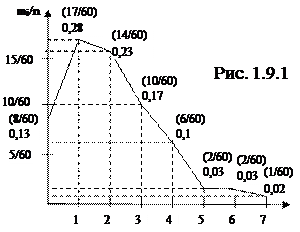
Для построения полигона относительных частот на оси абсцисс откладывают отдельные значения признака х_i. Из «принимаемых» значений х_i проводят перпендикуляры, длины которых пропорциональны относительным частотам w_i=m_i/n, затем концы соседних перпендикуляров соединяют отрезками прямых. Это полигон для статистического распределения выборки.

Пример 1.9.Полигон относительных частот числа неправильных соединений в минуту на АТС, построенный по таблице 1.5.1к примеру 1.5, приведен на рис. 1.9.1.

б) в случае непрерывного распределения случайной величины целесообразно строить гистограммы, которые также бывают двух видов: гистограммы частот и гистограммы относительных частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению m_i /h_i, (плотность частоты), где h_i –длина i-го интервала.

Гистограммастроится только для интервального вариационного ряда (группированной выборки). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы значений случайной величины. Затем на каждом частичном интервале, как на основании, строят прямоугольник с высотой, пропорциональной m_i /n.

Площадь i-го частичного прямоугольника равна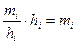– сумме частот вариантов i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки, а именно

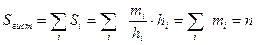
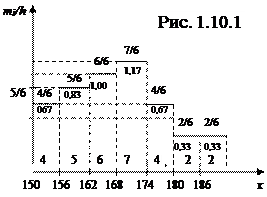
Пример 1.10.

На рис.1.10.1 изображена гистограмма частот для примера 1.6 (измерение роста студентов) по таблице 1.6.1.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению w_i /h (плотность относительной частоты), где w_i=m_i /n–относительные частоты случайной величины.

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы значений случайной величины. Затем на каждом частичном интервале, как на основании, строят прямоугольник с высотой, пропорциональной w_i/h.

Пример 1.11. На рис.1.11.1 изображена гистограмма относительных частот распределения для примера 1.6.

Площадь i-го частичного прямоугольника равна hw_i/h=w_i – относительной частоте вариантов i-го интервала; следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

в) кумулята – график накопленных частот, сглаженное графическое изображение эмпирической функции распределения, которая для каждого значения х определяет относительную частоту события, что Х<х, то есть, долю объектов совокупности, имеющих величину признака, менее заданной.

Если n – общее число наблюдений (объем выборки), n_x - число наблюдений, при которых наблюдалось значение признака, меньшее х, то относительная частота события, что Х<x равна n_х/n.

		Рис. 1.12.1