Б. Представление синусоидальных величин комплексными числами.

От представления синусоидальных величии вращающимися радиусами- векторами нетрудно перейти к представлению синусоидальных величин комплексными числами.

Для того чтобы представить синусоидальную величину

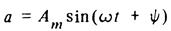
с начальной фазой Ψ комплексным числом, проведем на комплексной плоскости (рис. 6) из начала координат под углом Ψ к оси действительных величин и чисел вектор, длина которого в масштабе построения равна амплитуде Аm синусоидальной величины.

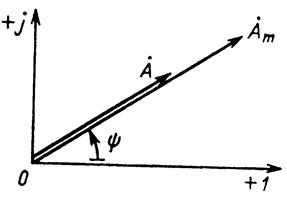
Рис. 6

Конец этого вектора находится в точке, которой соответствует определенное комплексное число - комплексная амплитуда синусоидальной величины:

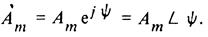
Так же обозначается и соответствующий комплексной амплитуде вектор на комплексной плоскости. При увеличении во времени фазы ωt+Ψ синусоидальной величины угол между вектором и осью действительных величин растет, т. е. получается вращающийся вектор

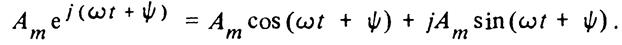
Нетрудно видеть, что мнимая часть вращающегося вектора равна заданной синусоидальной величине (3), По существу представление синусоидальной величины комплексной амплитудой Аm и соответствующим ей вектором на комплексной плоскости геометрически подобно представлению той же синусоидальной величины вращающимся радиусом-вектором 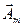в момент времени t = 0 (рис. 5, а). Поэтому может создаться впечатление, что оба представления синусоидальных величин практически совпадают. В действительности это не так. В случае представления синусоидальных величин комплексными числами можно применить весьма эффективный комплексный метод анализа электрических цепей синусоидального тока, который в настоящее время завоевал всеобщее признание.

Вектор на комплексной плоскости, длина которого в масштабе построения равна действующему значению синусоидальной величины, и соответствующее комплексное число называются комплексным действующим значением синусоидальной величины:

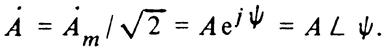
Так же обозначается и сам вектор на комплексной плоскости (рис. 6).

Применяются три формы записи комплексного значения

синусоидальной величины:

показательная форма

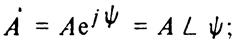
тригонометрическая форма

.

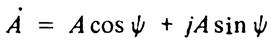и алгебраическая форма

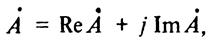
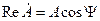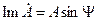где и - действительная и мнимая составляющие комплексного значения синусоидальной величины; ; .

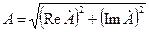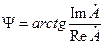Переход от показательной формы к тригонометрической выполнен при помощи формулы Эйлера:

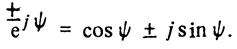
При значениях угла Ψ = π/2 и Ψ =-π/2 из формулы Эйлера следуют два часто встречающихся соотношения

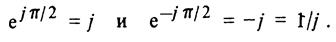
При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных величин; сокращенно их называют комплексными значениями, а соответствующие векторы на комплексной плоскости — векторами комплексных значений.