Выборки. Статистические оценки

В подавляющем большинстве случаев реальной практики закон распределения конкретной экспериментально наблюдаемой случайной величины, а также ее числовые характеристики s² и m исследователю не известны. Для установления точного вида закона распределения случайной величины или определения точных значений параметров ее распределения необходимо произвести обследование генеральной совокупности опытных данных.

Генеральной совокупностью называют воображаемое множество всех результатов испытаний, которые в принципе могут быть получены при данных условиях.

Генеральная совокупность может представлять собой либо бесконечно большое множество значений случайной величины (например, в случае измерения линейных размеров некоторого объекта количество измерений в принципе может быть бесконечным), либо ограниченное, конечное множество (например, в случае испытаний объектов исследования, приводящих к их разрушению, когда количество таких объектов ограничено).

Числовые характеристики случайной величины, рассчитанные при помощи всех данных генеральной совокупности, называют генеральными числовыми характеристиками. Они являютсядетерминированными, объективными характеристиками данной случайной величины.

На практике обычно имеется возможность провести только ограниченное число измерений, обследовав лишь часть генеральной совокупности, или выборку.

Выборкойназывают любое конечное подмножество генеральной совокупности, предназначенное для непосредственных исследований.

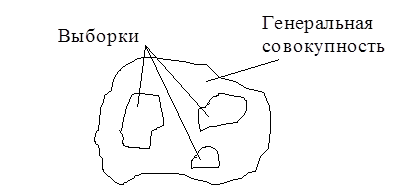
Рис. 2.6. Генеральная совокупность и выборка

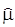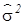Если, используя одни и те же выражения, произвести расчет числовых параметров распределения, сначала по данным генеральной совокупности (например, mи s²), а затем по данным выборки (соответственно обозначим и ), то окажется, что эти значения будут отличаться, причем отличаться тем больше, чем больше разница в объемах генеральной совокупности и выборки. При этом генеральные числовые характеристики (mи s²) будут иметь точные, строго и однозначно определенные (детерминированные) значения, так как для их определения использованы все возможные опытные данные и получить какие-либо другие значения в принципе невозможно. Рассчитанные же выборочные значения ( 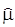и 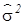) будут существенно зависеть от состава и объема выборки. Поскольку состав и объем выборки обычно определяется некоторым случайным образом, то и рассчитанные по выборке числовые параметры также будут иметь случайные значения, являясь по своей сути случайными величинами.

Эта разница в генеральных и выборочных характеристиках является принципиальной и определяет то, что величины, рассчитанные по выборке, являются некоторым приближением точных значений генеральных характеристик или оценками этих значений. Точность приближения (оценивания) зависит от количества испытаний N и местоположения опытных точек в генеральной совокупности.

Часто выборочные характеристики случайной величины называют статистиками, понимая под этим термином числовое значение, рассчитанное с использованием опытных данных.

Смысл всех статистических методов заключается в том, чтобы по выборке ограниченного объема (то есть по некоторой части генеральной совокупности) высказать обоснованное суждение о свойствах генеральной совокупности в целом. Наиболее часто такое суждение получают в процессе оценивания, в процессе построения оценок для неизвестных числовых характеристик генеральной совокупности случайной величины.

Различают два типа оценок генеральных числовых характеристик случайной величины: точечные оценки и интервальные оценки. Геометрически точечные оценки можно представить в виде точки на числовой оси оцениваемого генерального параметра распределения, расположенной вблизи заранее неизвестной точки, отражающей истинное значение этого параметра. Интервальные оценки можно представить в виде некоторого интервала значений, который накрывает оцениваемое значение с заданной вероятностью.

Точечные оценки получают в результате точечного оценивания.

Точечное оценивание – это определение приближенного значения неизвестного параметра генеральной совокупности по результатам наблюдений.

Для случайной величины с нормальным законом распределения наилучшими точечными оценками являются:

- для математического ожидания m – выборочное среднее арифметическое ;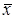

- для генеральной дисперсии s²– выборочная дисперсия s²;

- для генерального среднеквадратического отклонения s– выборочное среднеквадратическое отклонение s.

Выборочное среднее арифметическое – это сумма значений рассматриваемой величины, полученная по результатам испытания выборки, деленная на ее объем (количество единиц в выборке N):

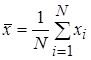. (2.14)

Выборочная дисперсия – это сумма квадратов отклонений выборочных результатов наблюдений от их выборочного среднего арифметического в выборке, деленная на (N-1) или N:

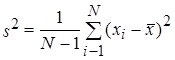. (2.15)

Формулу (2.15) удобно для практических расчетов на калькуляторе преобразовать к виду

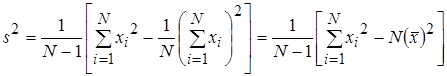. (2.16)

Выборочное среднеквадратическое отклонение – это положительный квадратный корень из выборочной дисперсии:

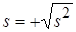. (2.17)

Величину, стоящую в знаменателе выражения для расчета выборочной дисперсии 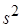(2.15), называют числом степеней свободы .

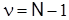Число степеней свободы – это разность между числом имеющихся выборочных экспериментальных значений (объемом выборки), по которым вычисляется оценка, и количеством дополнительных параметров, входящих в формулу для расчета оценки и вычисляемых в виде линейных комбинаций тех же самых значений.

При оценке дисперсии линейной комбинацией является выборочное среднее арифметическое, определяемое по выражению (2.14), и поэтому в выражении (2.15) для расчета выборочной дисперсии следует использовать именно .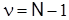

Интервальной оценкой неизвестного параметра распределения Q называется интервал ( 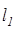, 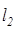), который с заданной вероятностью р накрывает оцениваемый параметр Q:

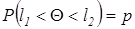. (2.18)

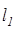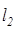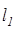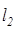Интервал ( , ) называется доверительными интервалом. Его границы и являются статистиками, так как рассчитываются по выборочным значениям, и называются соответственно нижним и верхним доверительными пределами. Ширина доверительного интервала L= 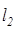- 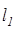является мерой точности оценки данного числового параметра.

Заданную вероятность р, используемую при построении доверительного интервала, называют доверительной вероятностью, а однозначно связанную с ней величину a=1-p – уровнем значимости. Доверительная вероятность характеризует степень достоверности, надежности результата, а уровень значимости a, наоборот, показывает степень неточности, ненадежности результата.

Доверительная вероятность р – это вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным.

При построении интервальной оценки значение доверительной вероятности р необходимо выбрать самостоятельно. При этом следует учитывать, что при увеличении значения р увеличивается степень доверия к оценке, но одновременно возрастает и ширина доверительного интервала, а следовательно, уменьшается точность получаемой оценки. Поэтому значение р принимают исходя из практической целесообразности. Наиболее часто используется значение доверительной вероятности р=0.95, реже – р=0.9ир=0.99.

Доверительный интервал принципиально может быть построен для любого параметра распределения. Наибольшее практическое значение имеют процедуры построения доверительных интервалов для математического ожидания, генеральной дисперсии и среднеквадратического отклонения.

Для случайной величины Х, подчиняющейся нормальному закону распределения с параметрами распределения m, σ² и σ, интервальные оценки строят при помощи нижеследующих выражений.

Интервальная оценка математического ожидания при известной дисперсии

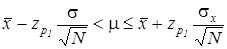, (2.19)

где 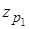– квантиль нормированного нормального распределения для доверительной вероятности Р₁=1-a/2,определяемая по табл. П.2.

Интервальная оценка математического ожидания при неизвестной дисперсии

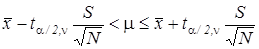, (2.20)

где t_a/2,n - значение квантили двустороннего распределения Стьюдента для уровня значимости a/2=(1-р)/2и числа степеней свободы n=N-1, определение которой можно произвести по табл. П.6.

Интервальная оценка генеральной дисперсии

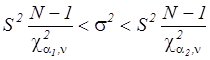, (2.21)

где 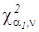и 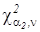– квантили распределения Пирсона для α₁=a/2 и α₂=1-a/2, (a=1-p), значения которых можно определить по табл. П.3.

Интервальная оценка генерального среднеквадратического отклонениястроится путем нахождения значений положительного квадратного корня из соответствующих границ для генеральной дисперсии.