Статистические гипотезы и критерии для их проверки
Одной из основных процедур получения выводов при использовании опытных данных является процедура проверки статистических гипотез.
Статистической гипотезой называют любое предположение, касающееся неизвестного распределения случайной величины в совокупности.
Идея формирования и проверки статистических гипотез состоит в следующем. Пусть для некоторого числового параметра распределения случайной величины Q по выборке объема N вычислена некоторая оценка 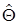 , называемая статистикой для проверки гипотез. Пусть имеется причина предположить, что истинное значение параметра Q, т.е. его значение в генеральной совокупности, равно Q0 . Это предположение следует проверить по имеющимся опытным данным выборки. Такое проверяемое предположение называют нулевой гипотезой (обозначают Н0) и записывают в виде соотношения Н0: Q=Q0. Даже если нулевая гипотеза справедлива, то статистика
, называемая статистикой для проверки гипотез. Пусть имеется причина предположить, что истинное значение параметра Q, т.е. его значение в генеральной совокупности, равно Q0 . Это предположение следует проверить по имеющимся опытным данным выборки. Такое проверяемое предположение называют нулевой гипотезой (обозначают Н0) и записывают в виде соотношения Н0: Q=Q0. Даже если нулевая гипотеза справедлива, то статистика 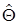 обычно не совпадает точно с Q0 , поскольку она является лишь одним из конкретных значений случайной величины
обычно не совпадает точно с Q0 , поскольку она является лишь одним из конкретных значений случайной величины 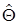 , порожденным случайной выборкой объема N. Если известна функция распределения оценки
, порожденным случайной выборкой объема N. Если известна функция распределения оценки 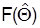 , построенная теоретически в предположении справедливости нулевой гипотезы, то с ее помощью с заданной доверительной вероятностью р можно построить доверительный интервал для оцениваемого параметра Q=Q0 (при проверке статистических гипотез доверительный интервал обычно называют областью принятия нулевой гипотезы). Области значений статистики
, построенная теоретически в предположении справедливости нулевой гипотезы, то с ее помощью с заданной доверительной вероятностью р можно построить доверительный интервал для оцениваемого параметра Q=Q0 (при проверке статистических гипотез доверительный интервал обычно называют областью принятия нулевой гипотезы). Области значений статистики 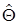 , не входящие в доверительный интервал, называют критической областью. Вероятность попадания статистики
, не входящие в доверительный интервал, называют критической областью. Вероятность попадания статистики 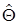 в критическую область a=1-рназываютуровнем значимости.Обычно такая вероятность имеет малое значение (0.05, 0.025 и т.п.).
в критическую область a=1-рназываютуровнем значимости.Обычно такая вероятность имеет малое значение (0.05, 0.025 и т.п.).
Рассчитанное по опытным данным действительное значение статистики 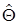 может попасть либо в область принятия нулевой гипотезы, либо в критическую область. Если
может попасть либо в область принятия нулевой гипотезы, либо в критическую область. Если 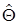 принадлежит области принятия нулевой гипотезы, то с вероятностью р следует считать нулевую гипотезу Н0: Q=Q0 справедливой. Если же
принадлежит области принятия нулевой гипотезы, то с вероятностью р следует считать нулевую гипотезу Н0: Q=Q0 справедливой. Если же 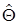 принадлежит критической области, то с вероятностью р нулевую гипотезу Н0 следует отвергнуть.
принадлежит критической области, то с вероятностью р нулевую гипотезу Н0 следует отвергнуть.
Нулевой гипотезой называют любую статистическую гипотезу, подлежащую проверке.
В большинстве реальных статистических ситуаций можно высказать сразу несколько гипотез. Обычно в качестве нулевой гипотезы используют гипотезу, наиболее вероятную или имеющую наиболее важное значение в проводимом исследовании.
Нулевую гипотезу выдвигают и затем проверяют с помощью статистических критериев в целях выявления оснований для ее отклонения и принятия альтернативной гипотезы.
Альтернативная гипотеза – это каждая допустимая гипотеза, отличная от нулевой.Ее обозначают НА или Н1.
Статистический критерий – однозначно определенный способ проверки статистических гипотез.
Такой способ (статистический критерий) включает в себя:
- формулу или способ расчета статистики, используемые для проверки данной конкретной нулевой гипотезы;
- известное теоретическое распределение, которому подчиняется данная статистика;
- способ определения границы критической области и способ определения местоположения критической области.
Статистикой для проверки гипотез называют функцию результатов наблюдений, составляющих выборку, однозначно связанную с принятым статистическим критерием и определяемую им.
Все возможные значения статистики для проверки гипотезы при помощи границы критической области делятся на две части: область принятия нулевой гипотезы и критическую область.
Критической областью называют область со следующими свойствами: если значения применяемой статистики принадлежит данной области, то отвергают нулевую гипотезу; в противном случае ее принимают.
По существу, проверка гипотезы сводится к выяснению того, в какую область попало рассчитанное значение статистики: если оно попало в критическую область, то нулевая гипотеза отвергается, а если в область принятия нулевой гипотезы, то принимается.
Наиболее часто границу критической области определяют по статистическим таблицам как квантиль некоторого известного теоретического распределения в зависимости от используемого критерия, принятого (самостоятельно в зависимости от целей исследования) уровня значимости α и числа степеней свободы ν.
Уровнем значимости называют вероятность отвергнуть объективно верную нулевую гипотезу (вероятность совершить ошибку первого рода). Наиболее часто принимают a=0.05, реже – a=0.01, a=0.1.
Критические области бывают односторонние и двусторонние. Смысл этих областей показан на рис. 2.7.
Если хотят убедиться в том, что одна случайная величина строго больше другой (или строго меньше другой), то используют одностороннюю критическую область.
В этом случае Н0: Q=Q0,
Н1: Q>Q0 или Н1: Q<Q0.
Если проверяют как положительные, так и отрицательные расхождения между изучаемыми величинами, то используют двусторонние критические области.
В этом случае Н0: Q=Q0,
Н1: Q¹Q0.
 Рис. 2.7. Критические области:
Рис. 2.7. Критические области:
а – правосторонняя; б – левосторонняя; в – двусторонняя
Всю процедуру проверки статистических гипотез можно в значительной степени формализовать, применяя один и тот же подход, определяемый некоторым алгоритмом, например следующим:
Алгоритм проверки статистических гипотез:
1) формулируют нулевую гипотезу Н0;
2) формулируют альтернативную гипотезу Н1;
3) выбирают критерий для проверки Н0;
4) рассчитывают статистику, относящуюся к выбранному критерию;
5) находят границы критической области при выбранной альтернативной гипотезе Н1, определяют местоположение критической области (слева или справа от границы);
6) проверяют попадание рассчитанной статистики в критическую область и делают вывод о справедливости выдвинутой нулевой гипотезы.
Из перечисленных процедур неформальными являются следующие:
- формулирование нулевой и альтернативной гипотез. Это одна из наиболее важных, сложных и ответственных процедур. Фактически она сводится к формализации поставленной задачи, описанию цели проведения исследования при помощи терминов и понятий, применяемых в математической статистике. Решение этой задачи достаточно эффективно может быть приведено только человеком, с одной стороны, хорошо знающим данную конкретную область (например, технологию и оборудование, применяемые для обработки металлов давлением), а с другой стороны, глубоко разбирающимся с вопросах статистического описания опытных данных;
- определение местоположения критической области (где она расположена, слева или справа от границы, определенной по таблице). Наиболее простое решение этого вопроса может быть получено следующим образом: 1) предположить, что нулевая гипотеза справедлива; 2) установить, какие значения при этом могут принимать случайные величины, входящие в формулу, для расчета статистики (удобно использовать некоторые предельные или граничные значения); 3) подставить эти значения в формулу для расчета статистики и рассчитать ее значение; 4) определить, в какую область (справа или слева от границы) попала статистика; 5) обозначить эту область как область принятия нулевой гипотезы, а другую область (отделенную границей) – как критическую.
Остальные процедуры, приведенные в алгоритме, по своей сути являются формальными и могут быть произведены с помощью справочных материалов.
В настоящее время в рамках теоретической и прикладной статистики известно большое количество методов анализа и сопоставления опытных данных, позволяющих получить вывод в очень широком спектре статистических ситуаций. Для этого разработано большое количество разнообразных статистических критериев. Небольшая часть таких ситуаций и критериев, широко и часто применяемых на практике, приведена в табл. 2.1. В таблице указаны применяемые в этих критериях статистики, правила определения границ критических областей и их местоположения. Для определения численных значений границ критических областей следует использовать соответствующие статистические таблицы, приведенные в приложении.
В таблице приняты следующие обозначения:
N – объем выборки (количество опытных данных);
ν – число степеней свободы;
α – уровень значимости;
μ – математическое ожидание, определяемое выражением (2.7);
s2 – генеральная дисперсия (2.8);
s – генеральное среднеквадратическое отклонение (2.9).
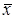 – выборочное среднее арифметическое (2.14);
– выборочное среднее арифметическое (2.14);
s2 – выборочная дисперсия (2.15);
s – выборочное среднеквадратическое отклонение (2.17).
Дата добавления: 2015-10-13; просмотров: 2672;
