Генеральная и выборочная дисперсия
Для того, чтобы охарактеризовать рассеяние значений количественного признака генеральной или выборочной совокупностей вокруг своих средних значений, вводят сводные характеристики - генеральную и выборочную дисперсии, соответственно.
Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения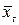 
.
Если все значения х1, х2, …, хN некоторого признака (параметра) генеральной совокупности объема N различны, то
Dг=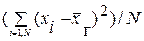 
Если же значения признака х1, х2, …, хk (k<n) имеют соответственно частоты M1, M2, …, Mk , причем M1 + M2 + … + Mk = N, то
Dr=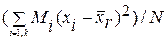 
т. е., генеральная дисперсия есть среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения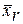 
,взвешенное весовыми коэффициентами, равными соответствующим частотам.
Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонений наблюдаемых значений признака выборочной совокупности от их среднего значения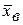 
.
Если все значения х1, х2, …, хN некоторого признака (параметра) выборочной совокупности объема n различны, то
Dв=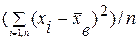 
т. е., выборочная дисперсия есть среднее арифметическое квадратов отклонений значений признака выборочной совокупности от их среднего значения .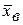
Если же значения признака х1, х2, …, хk (k<n) имеют соответственно частоты m1, m2, …, mk , причем m1 + m2 + … + mk = n, то
Dв=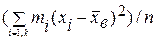 
то есть, выборочная дисперсия есть среднее арифметическое квадратов отклонений значений признака выборочной совокупности от их среднего значения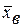 
,взвешенное весовыми коэффициентами, равными соответствующим частотам.
Генеральное и выборочное средние квадратичные отклонения определяются, соответственно, формулами
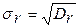и 
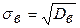
В качестве описательных характеристик вариационного ряда или полученного из него статистического распределения выборки еще используются
3) мода. Модой Мо дискретного вариационного ряда называется значение xi признака, имеющее наибольшее значение частоты mi.
Пример 13. Для вариационного ряда
со значениями признака 1 4 7 9
и частотами 5 1 20 6
мода равна 7.
Пример 14. Для вариационного ряда, рассмотренного в примере 1.4 (число неправильных соединений в минуту на АТС) мода равна 1. Укажем моду на графике полигона, приведенном на рис. 1.8.1.
Для интервального ряда находится интервал, у которого частота максимальна. Мода находится внутри интервального ряда. Для вычисления ее значения пользуются формулой линейной интерполяции. Например, для интарвельного ряда, рассмотренного в примере 1.6 (измерение роста студентов) мода находится в интервале [168, 174) Укажем моду на графике гистограмме, приведенном на рис. 1.10.1.
4) медиана. Медианой Ме вариационного ряда называется значение признака, приходящееся на середину ряда. Она делит вариационный ряд на две равные части, то есть, это серединная точка распределения, или такое значение признака (случайной величины), для которой половина принимаемых значений лежит слева от нее, а половина справа.
Для дискретного вариационного ряда медиана Ме определяется по формуле:
|
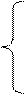
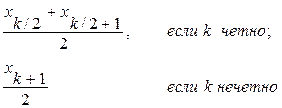
Пример 15. Для ряда 2 3 5 6 7 медиана равна 5;
для ряда 2 3 5 6 7 9 медиана равна (5+6)/2 = 5,5
Пример 16. Для вариационного ряда, приведенного на примере 1.4, значение k=8. Медиана для этого ряда равна Ме=(х4+х5)/2=(3+4)/2=3,5. Отметим медиану на рис. 1.8.1.
Для группированной выборки медиана – это точка, в которой площадь гистограммы делится пополам.
Пример 17.В примере 1.10 (рис. 1.10.1) половина площади гистограммы, равная 15, находится в конце интервала [162, 168), то есть, Ме = 168.
Если медиана лежит практически в центре области принимаемых значений случайной величины, она указывает на то, что у выборки нет сильного перекоса вправо или влево, она примерно симметрична относительно медианы. Сдвиг медианы вправо от центра области принимаемых значений или влево от этого центра (как на рис. 1.10.1) означает больший «вероятностный» удельный вес левой или, соответственно, правой половины принимаемых значений.
Дата добавления: 2015-11-06; просмотров: 3320;