Обычные, начальные и центральные эмпирические моменты
Часто в качестве параметров распределения вероятностей наблюдаемых значений признака рассматриваются моменты распределения (или функции от них). Моменты являются важными вероятностными характеристиками распределения.
Определяются два момента: начальный момент (а1), который по сути является математическим ожиданием распределения, относительно которого вычисляется второй момент, называемый центральным моментом b2, и по сути являющийся дисперсией.
Определение этих параметров аналогичны определениям соответствующих параметров теории вероятностей, но в отличие от них вычисляются по данным наблюдений.
Обычным эмпирическим моментом порядка k называют среднее значение k-х степеней разностей (xi – C):

где xi - значение (вариант) i-ой реализации наблюдаемой величины; mi – частота реализации данного значения; n = ∑mi - объем выборки, С – некоторое постоянное число, s – количество реализаций наблюдаемой величины.
Начальным эмпирическим моментом порядка k называют обычный момент порядка k при С=0
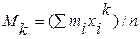
В частности, при k=1 имеем 
т.е. начальный эмпирический момент первого порядка равен выборочной средней (аналог математического ожидания)..
Центральным эмпирическим моментом порядка k называют обычный момент порядка k при 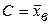

В частности, при k=1 имеем 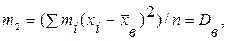 (1*)
(1*)
т.е. центральный эмпирический момент второго порядка равен выборочной дисперсии (аналог дисперсии).
Центральные моменты легко выражаются через обычные :
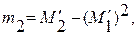 (1**)
(1**)
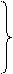
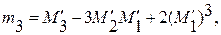 (1***)
(1***)
Дата добавления: 2015-11-06; просмотров: 2349;
