Моментов по условным

Определение центральных моментов требует довольно громоздких вычислений. Чтобы упростить расчеты, заменяют первоначальные моменты условными.

Условным эмпирическим моментом порядка k называют начальный момент порядка k, вычисленный для условных вариант (реализаций признака x_i):

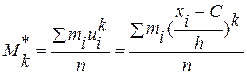
В частности

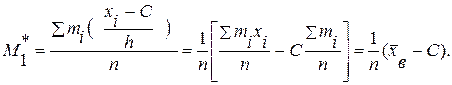
Отсюда 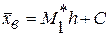(2*)

Таким образом, для того, чтобы вычислить выборочную среднюю, достаточно вычислить условный момент первого порядка, умножить его на h и к результату прибавить постоянную С.

Выразим обычные моменты через условные:

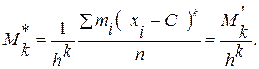
Отсюда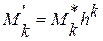

Таким образом, для того, чтобы найти обычный момент порядка k, достаточно условный момент того же порядка умножить на h_k.

Найдя обычные моменты, легко найти центральные моменты по равенствам (1**) и (1***). В итоге получим удобные для вычислений формулы, выражающие центральные моменты через условные:

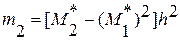(2**)

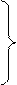
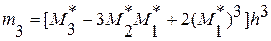
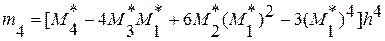
В частности, в силу (1**) и соотношения (1*) получим формулу для вычисления выборочной дисперсии по условным моментам первого и второго порядков (2****)

Моменты – очень важные характеристики распределения. Они намного проще функции распределения – это просто числа, но знание их дает очень много информации о распределении. Первый начальный момент (мат.ожидание) – это средняя точка распределения, тот «центр», вокруг которого все распределено. Второй центральный момент (дисперсия), характеризует разброс вокруг математического ожидания. Третий центральный момент, деленный на третью степень среднеквадратического отклонения – асимметрия, характеризует асимметрию распределения. Если он не равен нулю, то распределение несимметрично относительно своего центра. Четвертый центральный момент, деленный на четвертую степень среднеквадратического отклонения – эксцесс, характеризует «плосковершинность» распределения и т.д.