Наибольшее и наименьшее значения центральных моментов инерции.

Как известно, центральные моменты инерции являются наименьшими из всех моментов относительно ряда параллельных осей.

Найдем теперь крайние значения (максимум и минимум) для центральных моментов инерции. Возьмем ось 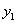, и начнем ее вращать, т. е. менять угол 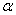; при этом будет изменяться величина

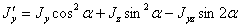
Наибольшее и наименьшее значения этого момента инерции соответствуют углу 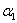, при котором производная 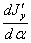обращается в нуль. Эта производная равна:

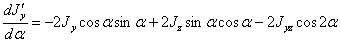
Подставляя в написанное выражение 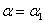и приравнивая его нулю, получаем:

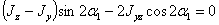
отсюда

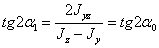
Таким образом, осями с наибольшим и наименьшим центральными моментами инерции будут главные центральные оси. Так как при повороте центральных осей сумма соответствующих моментов инерции не меняется, то

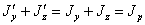
Когда один из центральных моментов инерции достигает наибольшего значения, другой оказывается минимальным, т, е. если

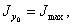то

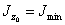
Следовательно, главные центральные оси инерции — это такие взаимно перпендикулярные оси, проходящие через центр тяжести сечения, относительно которых центробежный момент инерции обращается в нуль, а осевые моменты инерции имеют наибольшее и наименьшее значения.