ОСОБЕННОСТИ МАТЕМАТИЧЕСКИХ ВЫЧИСЛЕНИЙ, РЕАЛИЗУЕМЫХ НА ЭВМ: ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ: ПОГРЕШНОСТИ ВЫЧИСЛЕНИЙ

Современная вычислительная математика ориентирована на использование компьютеров для прикладных расчетов. Любые математические приложения начинаются с построения модели явления (изделия, действия, ситуации или другого объекта), к которому относится изучаемый вопрос. Классическими примерами математических моделей могут служить определенный интеграл, уравнение колебаний маятника, уравнение теплообмена, уравнения упругости, уравнения электромагнитных волн и другие уравнения математической физики. Назовем еще для контраста модель формальных рассуждений – алгебру Буля.

Основополагающими средствами использования математических моделей являются аналитические методы: получение точных решений в частных случаях (например, табличные интегралы), разложения в ряды. Определенную роль издавна играли приближенные вычисления. Например, для вычисления определенного интеграла использовались квадратурные формулы.

Появления в начале XX века электронных вычислительных машин (компьютеров) радикально расширило возможности приложения математических методов в традиционных областях (механике, физике, технике) и вызвало бурное проникновение математических методов в нетрадиционные области (управление, экономику, химию, биологию, психологию, лингвистику, экологию и т.п.).

Компьютер дает возможность запоминать большие (но конечные) массивы чисел и производить над ними арифметические операции и сравнения с большой (но конечной) скоростью по заданной вычислителем программе. Поэтому на компьютере можно изучать только те математические модели, которые описываются конечными наборами чисел, и использовать конечные последовательности арифметических действий, а также сравнений чисел по величине (для автоматического управления дальнейшими вычислениями).

В традиционных областях математическими моделями служат функции, производные, интегралы, дифференциальные уравнения. Для использования компьютеров эти исходные модели надо приближенно заменить такими, которые описываются конечными наборами чисел с указанием конечных последовательностей действий (конечных алгоритмов) для их обработки. Например, функцию следует заменить таблицей; производную

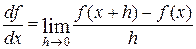
Заменить приближенной формулой

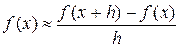
определенный интеграл - суммой; краевую задачу для дифференциального уравнения - задачей об отыскании таблицы значений решения в узлах некоторой сетки, причем так, чтобы выбор шага сетки позволял достигать любой требуемой точности. Оказывается, из двух, на первый взгляд равноценных способов один может оказаться принципиально непригодным из-за того, что доставляемое им приближенное решение не стремится к искомому при измельчении шага сетки, или из-за катастрофически сильной чувствительности к погрешностям округления.

Теория таких моделей и алгоритмов составляет предмет вычислительной математики. Эта теория тесно связана с теориями приближения и интерполяции функций, уравнений с частными производными, интегральных уравнений, информационной сложности функциональных классов, алгоритмов, а также с языками программирования для расчетов на компьютере и т. д. Современные вычислительные методы позволяют, например, рассчитать характеристики обтекания газом тела заданной формы, что недоступно аналитическим методам (подобно нетабличному интегралу).

С использованием компьютера стал возможен вычислительный эксперимент, т. e. расчет в целях проверки гипотез, а также в целях наблюдения за поведением модели, когда заранее не известно, что именно заинтересует исследователя. В процессе численного эксперимента происходит по существу уточнение исходной математической постановки задачи. В процессе расчетов на компьютере происходит накопление информации, что дает возможность в конечном счете произвести отбор наиболее интересных ситуаций. На этом пути сделано много наблюдений и открытий, стимулирующих развитие теории и имеющих важные практические применения.

С помощью компьютера возможно применение математических методов и в нетрадиционных областях, где не удается построить компактные математические модели вроде дифференциальных уравнений, но удается построить модели, доступные запоминанию и изучению на компьютере. Модели для компьютеров в этих случаях представляют собой цифровое кодирование схемы, изучаемого объекта (например, языка) и отношений между его элементами (словами, фразами). Сама возможность изучения таких моделей на компьютере стимулирует появление этих моделей, а для создания обозримой модели необходимо выявление законов, действующих в исходных объектах. С другой стороны, получаемые на компьютере результаты (например, машинный перевод упрощенных текстов с одного языка на другой) вносят критерий практики в оценку теорий (например, лингвистических теорий), положенных в основу математической модели.

Благодаря компьютерам стало возможным рассматривать вероятностные модели, требующие большого числа пробных расчетов, имитационные модели, которые отражают моделируемые свойства объекта без упрощений (например, функциональные свойства телефонной сети).

Разнообразие задач, где могут быть использованы компьютеры, очень велико. Для решения каждой задачи нужно знать многое, связанное именно с этой задачей. Естественно, этому нельзя научиться впрок.

Целью курса является сообщение тех основных понятий, идей и методов, владение которыми позволяет сравнительно быстро научиться работать в конкретных областях. Это реализуется на материале вычислительных задач алгебры, математического анализа, дифференциальных уравнений, поскольку здесь методы хорошо развиты и применяются в далеких друг от друга областях.

Назовем некоторые общие понятия и идеи, которые требуют внимания и наполняются конкретным содержанием в зависимости от задачи, которую предстоит решать с помощью компьютера. Это - дискретизация задачи; обусловленность задачи; погрешность численного метода; вычислительная устойчивость алгоритма; сравнение алгоритмов по полноте используемой ими входной информации, по используемой памяти и числу арифметических действий. Алгоритмы могут отличаться возможностью распараллеливания для одновременного проведения вычислений на многопроцессорном компьютере. Одним из плодотворных и основных методов вычислительной математики является комбинированное использование аналитических и компьютерных средств.

Во введении рассматриваются перечисленные понятия. Это даст некоторое общее представление о предмете вычислительной математики и подготовит к изучению дальнейшего материала.

Дискретизация

Пусть требуется найти приближенное решение какой-либо задачи, в которой в качестве входных данных участвует какая-либо функция f(x), определенная на всем (бесконечном) множестве точек отрезка 0≤x≤1. Значения этой функции при каждом фиксированном x можно получить измерениями или вычислениями. Для запоминания этой функции в памяти компьютера необходимо приближенно описать ее таблицей значений на некотором конечном множестве отдельных точек 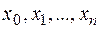. Это – простейший пример дискретизации задачи: от задачи запоминания функции на отрезке [0, 1] мы перешли к задаче запоминания таблицы значений на дискретном множестве точек 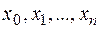из этого отрезка.

Пусть функция f(x), имеет достаточное число производных, а нам требуется вычислить ее производную , в данной точке x. Задачу отыскания

,

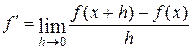содержащую предельный переход, можно заменить приближенно задачами вычисления по одной из формул

(1.1)

(1.2)

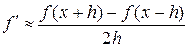(1.3)

Для замены производной 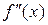можно воспользоваться формулой

(1.4)

Все эти формулы уточняются при уменьшении h, а при каждом фиксированном h определены для конечных наборов значений функции и используют только арифметические операции. Эти формулы – примеры дискретизации задачи о вычислении производных , .

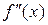Рассмотрим краевую задачу

(1.5)

y(0) = 2, y(1) = 3,

Об отыскании функции y(x), определенной на отрезке . Для построения приближенной дискретной модели этой задачи осуществим следующие два шага.

Разобьем отрезок на N равных частей длины 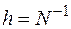каждая, а вместо функции y(x) будем искать набор значений 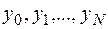этой функции в точках 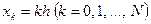. В точках 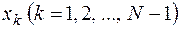заменим производную 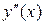приближенно по формуле (4) и получим

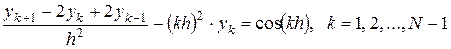(1.6)

Кроме того, в силу граничных условий (5) положим

. (1.7)

Система N+1 линейных уравнений (1.6), (1.7) относительно того же числа неизвестных 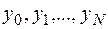является дискретным аналогом задачи (1.5).

Есть основания думать, что с ростом N решение задачи (1.6), (1.7) есть все более точная таблица значений решения задачи (1.5) (в дальнейшем это будет показано).

Обозначим континуальную краевую задачу через 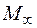, а дискретную краевую задачу (1.6), (1.7) через 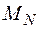. Тогда можно сказать, что задаче 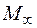мы сопоставили бесконечную последовательность дискретных задач 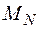(N=2,3,…).

Вычисляя решение задачи 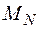при каком-либо фиксированном N, мы имеем дело с конечным набором чисел, задающих входные данные, и с конечным набором чисел 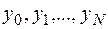, подлежащих отысканию. Однако вычислительная математика обычно ставит своей целью предложить именно последовательность уточняющихся дискретных моделей 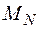, так как это дает возможность выбрать то N, которое обеспечивает выполнение требований к точности.

Переход от континуальной задачи 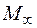к последовательности 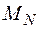ее дискретных моделей возможен многими способами. Пусть 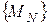, – какие-нибудь две последовательности таких моделей, причем вычисления решений дискретных задач 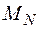и требует равных затрат. Тогда предпочтение надо отдать тому способу дискретизации, при котором решение дискретной задачи может служить решением исходной задачи с заданной точностью при меньшем значении N.

Бывает, что из двух, казалось бы, равноценных способов дискретизаци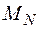и и один при возрастании N дает все более точное приближение к решению континуальной задачи 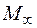, а другой приводит к “приближенному решению” задачи, которое с ростом N теряет какое-либо сходство с искомым решением.

1.2. Обусловленность

Во всякой задаче требуется по входным данным сделать заключение о каких-либо свойствах решения. Похожие на первый взгляд задачи могут резко отличаться чувствительностью интересующих свойств решения к возмущению входных данных. Если это чувствительность “мала”, то задача считается хорошо обусловленной; в противном случае – плохо обусловленной. Обычно плохо обусловленные задачи не только предъявляют высокие требования к точности задания входных данных, но и более трудны для вычислений.

Пример. Пусть концентрация y = y(t) некоторого вещества в момент времени t есть функция, удовлетворяющая дифференциальному уравнению

.

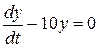Фиксируем произвольно 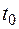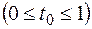и делаем приближенное измерение 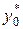концентрации 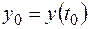, получим

.

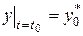Задача состоит в определении концентрации y = y(t) в произвольный момент времени t из отрезка .

Если бы число 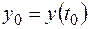было известно точно, то можно было бы указать точную формулу

для концентрации. Но мы знаем лишь приближенное значение 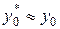числа . Поэтому вместо мы можем указать лишь приближенную формулу . Очевидно, что погрешность выражается формулой

.

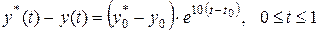Допустим, нам нужно произвести замер 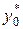с такой точностью 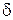, , 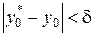чтобы гарантировать некоторую заданную точность 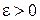всюду на отрезке , т.е. гарантировать оценку

.

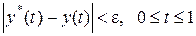Очевидно,

.

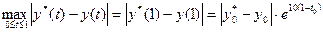Отсюда получаем следующее требование к точности δ измерения y₀ :

.

Пусть измерение производится в момент .Тогда требование к точности 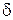измерения будет в 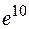раз, т.е. в тысячи раз выше, чем требуемая гарантированная точность ε результата. Ответ весьма чувствителен к погрешности задания входных данных, т. е. , и задача плохо обусловлена.

Если измерение производить при 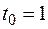, то 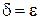, т. е. достаточно измерение с гораздо меньшей точностью, чем в случае , и задача хорошо обусловлена.

Задача

На каком из двух отрезков x: 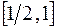или[-1, 0], задача вычисления лучше обусловлена.

Погрешность

Во всякой вычислительной задаче по некоторым входным данным задачи требуется найти ответ на поставленный вопрос. Если ответ на вопрос задачи можно дать с абсолютной точностью, то погрешность отсутствует. Но обычно удается найти ответ лишь с некоторой погрешностью. Погрешность вызывается тремя причинами.

Первая причина – некоторая неопределенность при задании входных данных, которая приведет к соответствующей неопределенности в ответе: ответ может быть указан лишь с некоторой погрешностью, которая носит название неустранимой погрешности.

Вторая причина: если мы ликвидируем неопределенность в задании входных данных, фиксировав какие-либо входные данные, а затем будем вычислять ответ с помощью какого-нибудь приближенного метода, то найдем не в точности тот ответ, который соответствует этим фиксированным входным данным. Возникает погрешность, связанная с выбором приближенного метода вычислений.

Третья причина: сам выбранный нами приближенный метод реализуется неточно из-за погрешностей округлений при вычислениях на реальном компьютере.

Погрешность результата складывается, таким образом, из неустранимой погрешности, погрешности метода и погрешности округлений.

Проиллюстрируем эти понятия.

1.Неустранимая погрешность. Пусть задача состоит в вычислении значения y некоторой функции y = f(x) при некотором x = t. Число t и соответствие f, в силу которого каждому значению аргумента сопоставляется значение функции, служат входными данными задачи, а число y(t) – решением.

Пусть функция f(x) известно лишь приближенно, например, , причем известно лишь, что f(x) отличается от 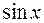не более, чем на некоторую величину :

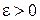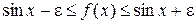. (1.8)

Пусть значение аргумента x = t получается приближенным измерением, в результате которого получаем некоторое , причем известно лишь, что t лежит в пределах

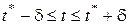(1.9)

где – число, характеризующее точность измерения.

Из рис. 1 видно, что величиной y = f(t) может оказаться любая точка отрезка [a, b], где , 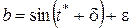(примечание: f(t) – возрастающая). Понятно, что, приняв за приближенное значение числа y = f(t) любую точку 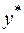отрезка [a, b], можно гарантировать оценку погрешности

. (1.10)

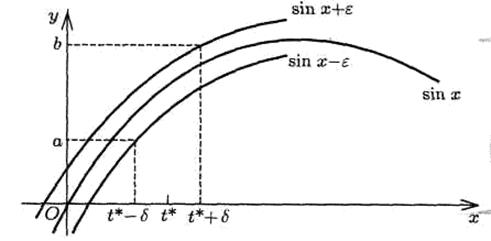
Рис. 1 – Оценка неустранимой погрешности

Эту оценку погрешности нельзя существенно уменьшить при имеющихся неполных входных данных. Самая малая погрешность, которую можно гарантировать, получается, если принять за 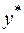середину отрезка [a, b], положив

.

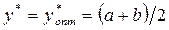Из рис. 1 видно, что гарантирована оценка

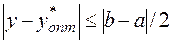. (1.11)

Это неравенство станет точным равенством, если y(t) = a или y(t) = b.

Таким образом, 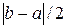и есть та неустранимая (неуменьшаемая) погрешность, которую можно гарантировать при имеющихся неопределенных входных данных в случае самого удачного выбора приближенного решения _.

Оптимальная оценка (1.11) ненамного лучше оценки (1.10). Поэтому мы отступим от здравого смысла, если о любой точке , а не только о точке _, условимся говорить, что она есть приближенное решение задачи вычисления числа y(t), найденное с неустранимой погрешностью, а вместо 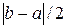из (4) за величину неустранимой погрешности примем (условно) число .

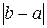2.Погрешность метода. Положим 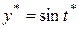. Число 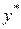принадлежит отрезку [a, b] и является неулучшаемым приближенным решением задачи, погрешность которого удовлетворяет оценке (1.3) и неустранима. Точка 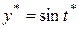выбрана среди других точек отрезка [a, b], потому что она задается удобной для дальнейшей работы формулой.

Для вычисления числа 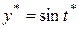на компьютере воспользуемся разложением функции 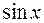в ряд:

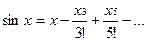
(1.12)

Для вычисления 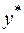можно воспользоваться одним из приближенных выражений

,

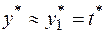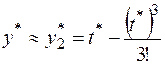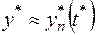, (1.13)

…

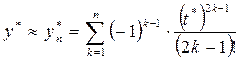
Выбирая для приближенного вычисления 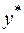одну из формул (1.6), мы тем самым выбираем метод вычисления.

Величина 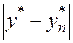есть погрешность метода вычислений.

Фактически выбранный нами метод вычисления зависит от параметра n и позволяет добиваться, чтобы погрешность метода была меньше любой наперед заданной величины за счет выбора этого параметра.

Очевидно, нет смысла добиваться, чтобы погрешность метода была существенно (во много раз) меньше неустранимой погрешности. Число n поэтому нет смысла брать слишком большим. Однако в случае, если n выбрано слишком маленьким так, что погрешность метода существенно больше неустранимой погрешности, то избранный метод не полностью использует информацию о решении, содержащуюся во входных данных, теряя часть этой информации.

3.Погрешность округлений. Допустим, мы фиксировали метод вычислений, положив 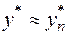. При вычислении 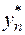по формуле (1.13) на реальном компьютере в результате округлений мы получим некоторое число 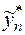. Погрешность будем называть погрешностью округлений.

Эта погрешность не должна быть существенно больше погрешности метода вычислений. В противном случае произойдет потеря точности метода за счет погрешностей округлений.

Задачи

1. Пусть требуется вычислить значение y = f(x) функции f(x) по неполным входным данным .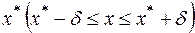

Какова неустранимая погрешность, вызванная неполным значением входных данных, в зависимости от и :

a) ;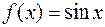

b) ?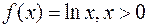

При каких значениях , полученных приближенным измерением неопределенной величины x с погрешностью 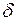, в задаче б) можно указать лишь одностороннюю оценку для 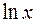сверху. Укажите эту оценку.

2. Задана некоторая функция y = f(x), о которой известно, что ее вторая производная по модулю не превосходит единицы.

Показать, что погрешность приближенного равенства

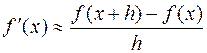
не превосходит величину h.

3.Пусть некоторая функция y = f(x) имеет вторую производную 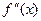, которая по модулю не превосходит единицы. При каждом x значение f(x) получается приближенным измерением величины f(x) и оказывается равным некоторому числу 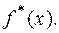Пусть известно лишь, что точность измерения гарантирует справедливость оценки

,

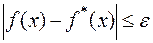где – число, характеризующее точность измерений. Пусть требуется приближенно вычислить f^’(x).

Как выбрать h, чтобы гарантированная погрешность приближенной формулы

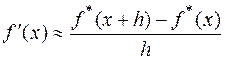
была наименьшей?