Устойчивость и сложность алгоритма (по памяти, по времени)

Пусть для изучения некоторого объекта построена его математическая модель, которая и подлежит изучению средствами вычислительной математики.

Например, математической моделью малых колебаний маятника может оказаться следующая задача:

,

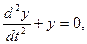
y(0) = 0, 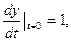(1.14)

где y(t) – отклонение маятника в момент времени t.

При изучении гармонических колебаний с помощью этой математической модели, т. е. задачи Коши (1.14), некоторую пользу может принести знание физической сущности моделируемого физического объекта. В данной задаче, например, можно предвидеть, что решение носит колебательный (периодический) характер. Однако математическая модель (1.14) после ее построения становится самостоятельным объектом, для изучения которого можно применять любые математические средства, в том числе и те, которые не имеют никакого отношения к физическому происхождению задачи. Это сильно расширяет возможности исследователя. Так, например, значение решения 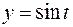задачи (1.14) в заданной момент времени t = z, т. е. представление числа в виде десятичной дроби с заданным числом знаков, можно осуществить с помощью ряда

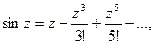
воспользовавшись его частичной суммой.

Между тем представление функции в виде степенного ряда, использованное нами, не имеет никакого физического смысла.

Для численного решения какой-либо задачи на компьютере возможны различные численные методы, или различные алгоритмы. Однако из них могут быть много лучше других.

В этой книге мы изложим хорошие алгоритмы для многих часто встречающихся классов задач, а пока объясним, чем могут различаться алгоритмы.

Пусть для вычисления решения y некоторой задачи по входным данным, совокупность которых обозначим X, имеются алгоритмы , , 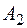которые дают приближения 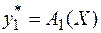, 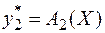. При этом может оказаться следующее.

1.Алгоритм 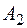может быть точнее алгоритма , т. е.

.

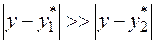Например, будем вычислять по формуле вида

(1.15)

Примем за алгоритм, отвечающий n =1, а за 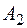алгоритм, отвечающий n =2. Очевидно, что

.

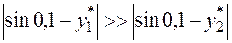2. Алгоритмы обладают одинаковой точностью, но вычисление 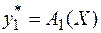требует много больше арифметических действий, чем вычисление .

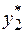Пусть, например, требуется найти

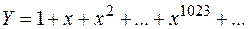
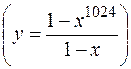
при х = 0,99. За примем алгоритм, осуществляющий вычисления прямо по заданной формуле, возводя 0,99 поочередно в степени 1, 2, …, 1023 и складывая. В качестве 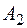примем алгоритм, осуществляющий вычисление по формуле

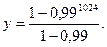
По точности алгоритмы совпадают (оба абсолютно точно), но первый требует гораздо больше арифметических операций.

А именно, вычисляя последовательно 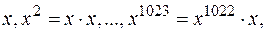придется проделать 1022 умножения. В то же время при вычислении требуется всего 10 умножений:

.

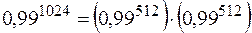3. Алгоритмы обладают одинаковой точностью, но вычислительно устойчив, а неустойчив.

Например, для вычисления с заданной точностью воспользуемся суммой

(1.16)

где выбирается так, чтобы выполнялось неравенство

,

Приняв вычисления этой суммы за алгоритм . Если , то

.

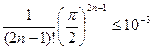При n = 5, и

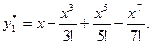
Очевидно, что вычисления по этой формуле слабо реагируют на погрешности округления при вычисления каждого из слагаемых, а поэтому алгоритм в данном случае вычислительно устойчив.

Пусть ; например, х = 100. Тогда для достижения требуемой точности число n должно удовлетворять неравенству:

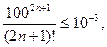
из которого для n заведомо выполнено неравенство n > 48. Но при вычислении суммы (16) первые ее члены будут очень большими. Малая относительная погрешность при их вычислении дает большую абсолютную погрешность, и алгоритм вычислительно неустойчив.

Укажем устойчивый алгоритм . Записываем заданное х в виде 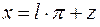, ( , l целое). Тогда

,

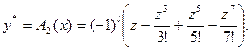
Этот алгоритм по устойчивости совпадает с алгоритмом 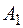для .

4.Алгоритм может быть сходящимся или расходящимся.

Пусть требуется вычислить 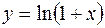. Воспользуемся рядом

(1.17)

и положим

Получим метод вычисления 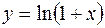, зависящий от номера n как от параметра.

Если 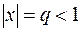, то 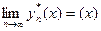, т. е. погрешность алгоритма с ростом n стремится к нулю. Но если x > 1, то , так как ряд (1.17) имеет радиус сходимости r =1. В этом случае алгоритм непригоден для вычислений.

В книге мы познакомимся и с некоторыми другими характеристиками алгоритмов. Встретятся алгоритмы вычисления или требующие последовательного выполнения операций, самонастраивающиеся на специфику входных данных или учитывающие ее лишь отчасти алгоритмы логически простые или более сложные.

2. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Численные методы решения задач линейной алгебры в значительной степени объединяет система понятий и идентичность подходов к решению задач.

Сначала приводятся численные методы решения систем линейных алгебраических уравнений. В линейной алгебре эту задачу называют первой основной задачей. К ней примыкают задачи вычисления определителей и элементов обратной матрицы, которые иногда называют второй и третьей основными задачами линейной алгебры.

Далее излагаются численные методы уточнения корней нелинейных уравнений. В общем случае такие уравнения не имеют аналитических формул для своих корней или эти формулы слишком громоздки и неудобны для практического использования. В частности, в начале 19 века было доказано, что нелинейные уравнения выше четвертой степени неразрешимы в радикалах даже при использовании радикалов произвольной степени. Используемые численные методы уточнения корней нелинейных уравнений можно условно разделить на две группы. К первой группе относятся методы, которые назовем универсальными в том смысле, что в принципе они пригодны для отыскания корней уравнений любого вида. Эти методы носят итерационный характер. Подробно рассмотрены метод дихотомии (деления пополам), метод простой инерции, метод Ньютона и две его модификации: метод секущих и метод Ньютона с постоянным значением производной. Кратко дан метод парабол.

Для системы нелинейных уравнений приведено обобщение методов простой итерации, метода итераций Зейделя и метода Ньютона в приложении к одному нелинейному уравнению.

Основные понятия линейной алгебры. Классификация методов решения

Приведем некоторые сведения из линейной алгебры, которые потребуются в дальнейшем. Рассмотрим прямоугольную матрицу

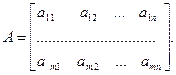
Две матрицы к и 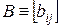размерности 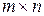равны друг другу, если 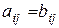для всех i и j.

Сумма двух матриц А и В размерности 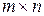есть матрица размерности :

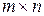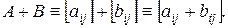
Произведение матрицы А на скаляр α есть матрица размерности :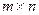

Введем обозначение Произведение матрицы А размерности 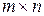на матрицу В размерности 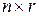есть матрица С размерности :

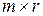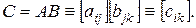
Таким образом, элемент 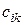матрицы С есть сумма произведений i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В, при этом число столбцов матрицы А должно равняться числу строк матрицы В. Из существования произведения АВ вовсе не следует существование произведения ВА. Для квадратных матриц (m=n) одного порядка существуют матрицы АВ и ВА, но, вообще говоря, .

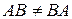ОПРЕДЕЛИТЕЛЬ (ДЕТЕРМИНАНТ) квадратной матрицы будем обозначать det A:

.

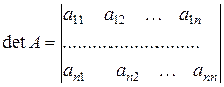Определитель квадратной матрицы с элементами (действительными или комплексными числами ) есть сумма n! членов вида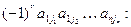

где – алгебраическое дополнение элемента . Отметим, что (неравенство Адамара).

Важным частным случаем квадратной матрицы является ДИАГОНАЛЬНАЯ МАТРИЦА

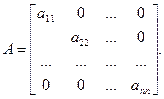
При МАТРИЦА называется ЕДИНИЧНОЙ и обозначается через Е. Другим частным случаем квадратной матрицы является ТРЕХДИАГОНАЛЬНАЯ МАТРИЦА

.

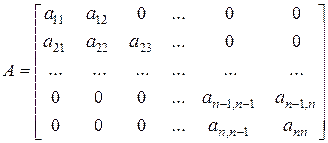С такими матрицами часто приходится иметь дело при решении дифференциальных уравнений. Матрица называется НИЖНЕЙ ТРЕУГОЛЬНОЙ, если все ее элементы, расположенные выше главной диагонали, равны нулю:

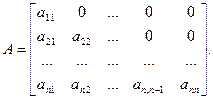
Аналогично определяется ВЕРХНЯЯ ТРЕУГОЛЬНАЯ матрица. Квадратная матрица называется СИММЕТРИЧНОЙ, если ее элементы удовлетворяют соотношению 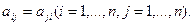Если в матрице поменять строки со столбцами, то получим транспонированную матрицу

Квадратная матрица А симметрична, если .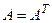

Обозначим через х вектор-столбец и через 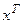– вектор-строку. Матрица называется ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННОЙ, если .

Матрица 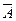называется КОМПЛЕКСНО СОПРЯЖЕННОЙ с матрицей А, если ее элементы суть комплексно сопряженные с элементами матрицы А. Матрица 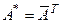называется сопряженной с матрицей А. Если матрица А вещественная, то ^.

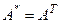Матрица называется ОБРАТНОЙ матрице А, если . Необходимым и достаточным условием существования обратной матрицы является условие 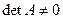. Говорят, что в этом случае матрица А несобственная, или невырожденная.

МИНОРОМ порядка k матрицы А называется определитель k-го порядка, составленный из элементов, которые находятся на пересечении k строк и k столбцов матрицы А. РАНГОМ матрицы А называется число r такое, что все миноры порядка r + 1 и выше равны нулю.

ХАРАКТЕРИСТИЧЕСКИМ УРАВНЕНИЕМ матрицы А называется уравнение

Корни 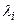этого уравнения называются СОБСТВЕННЫМИ ЧИСЛАМИ матрицы А. Левая часть уравнения 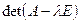называется характеристическим полиномом. СОБСТВЕННЫМ ВЕКТОРОМ матрицы А называется отличный от нуля вектор, удовлетворяющий условию .

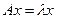Две квадратные матрицы А и В называются ПОДОБНЫМИ, если , где S - невырожденная матрица и 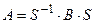. Подобные матрицы имеют одинаковые характеристические многочлены и, следовательно, одинаковые собственные значения и определители, так как 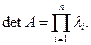Собственные векторы матрицы А связаны с собственными векторами матрицы В соотношением х = Ву. Матрица А невырожденная, если все 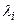отличны от 0. Все собственные числа симметричной матрицы действительны.

Действительная матрица называется ОРТОГОНАЛЬНОЙ, если ее транспонированная матрица совпадает с обратной, т. е. 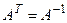или 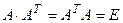. Все собственные значения ортогональной матрицы по модулю равны единице. Строки (столбцы) ортогональной матрицы попарно ортогональны, суммы квадратов элементов каждой строки (столбца) ортогональной матрицы равны единице, определитель ортогональной матрицы равен 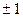; если матрица А ортогональна, то и матрица тоже ортогональна.

Всякая симметричная действительная матрица может быть приведена к диагональному виду подобным преобразованием

,

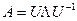где U – ортогональная матрица, 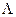- диагональная матрица. Из свойств ортогональной матрицы следует, что

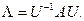
В дальнейшем зачастую рассматриваются множества, элементами которых являются числа, векторы, матрицы, функции. Сами множества обычно являются линейными нормированными пространствами, ибо в них определены операции сложения элементов и их умножения на число и введена норма каждого элемента 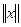. НОРМОЙ называется вещественное неотрицательное число, удовлетворяющее следующим условиям:

• при х 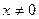, 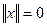при х = 0.

•

•

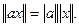
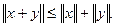
Рассмотрим нормы в некоторых множествах. В множестве действительных чисел 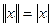. В множестве функций х(t), определенных и непрерывных при 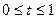(пространство С), определена чебышевская норма 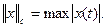В конечномерном пространстве, элементами которого являются группы из n чисел 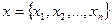(их можно считать координатами векторов), норма определена следующим образом:

.

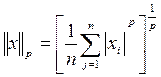Между разными нормами существует соотношение

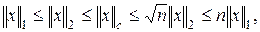
где по аналогии с пространством С. Поэтому из сходимости в одной из норм следует сходимость в остальных.

В пространстве квадратных матриц порядка n наиболее употребительны следующие нормы:

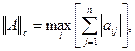
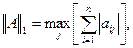
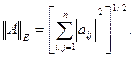
Норма 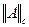- максимальное число среди сумм модулей элементов строк матрицы, норма 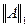- максимальное число среди сумм модулей элементов столбцов матрицы. Эти нормы не имеют специального названия, норма 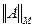называется максимальной, а 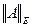- сферической или евклидовой. Необходимо отметить, что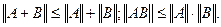

Интересна связь между нормами матриц и векторов, на которые матрицы действуют. Норма матрицы называется согласованной с нормой вектора, если 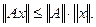Сферическая норма согласована с 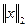, а максимальная согласована со всеми рассмотренными выше нормами.

Введем понятие предела векторов и матриц. Рассмотрим последовательность векторов 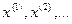с компонентами Если существуют пределы 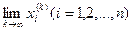, то говорят, что вектор с компонентами 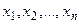является пределом последовательности матриц. Необходимым и достаточным условием сходимости векторов 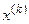к x является условие 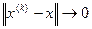, при этом 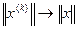. Аналогичное утверждение справедливо для матриц.

Требуется найти решение системы линейных уравнений

Ax = b, (2.1)

где – квадратная матрица коэффициентов при неизвестных; 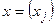– вектор-столбец неизвестных; – вектор-столбец правых частей системы. С точки зрения классической теории линейных алгебраических систем их решение не вызывает затруднений. По правилу Крамера системы n неизвестными имеет единственное решение, если определитель системы отличен от нуля 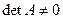и значение каждого из неизвестных вычисляется как отношение двух определителей порядка n, т. е.

j =1, …, n. (2.2)

Здесь 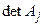– определитель матрицы, получаемый заменой j-го столбца матрицы А столбцом правых частей. При непосредственном вычислении определителей как алгебраической суммы n! произведений элементов для отыскания решения системы линейных уравнений по правилу Крамера требуется приблизительно 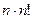арифметических операций типа умножения. Будет показано, что использование метода исключения Гаусса позволяет уменьшить время, необходимое для решения задачи (2.1), до величины менее одной секунды.

Другое важное обстоятельство, связанное с решением систем линейных алгебраических уравнений, состоит в следующем. С точки зрения теории линейных систем различаются два случая: определитель матрицы системы не равен нулю ( 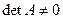), т. е. система уравнений является невырожденной, либо определитель матрицы системы равен нулю (detA = 0), в этом случае система называется вырожденной. Во втором случае система либо не имеет решения (при ), либо имеет неединственное решение (при b = 0). С точки зрения практических вычислений существуют “почти невырожденные системы” – системы, определитель которых близок к нулю, но отличен от нуля ( 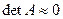). Небольшие изменения коэффициентов матрицы системы или правых частей системы в “почти невырожденных системах” могут привести к большим погрешностям решения.

Все эти случаи хорошо иллюстрируются на примере решения системы двух линейных уравнений:

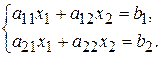
На рисунке 2 каждому уравнению соответствует прямая на плоскости ,а точка пересечения этих прямых есть решение системы (2.1).

Если det A = 0, то наклоны прямых равны и они либо параллельны, либо совпадают. При 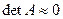небольшие погрешности в коэффициентах и правых частях могут привести к большим погрешностям в решении, т. е. к неточному определению положения точки пересечения.

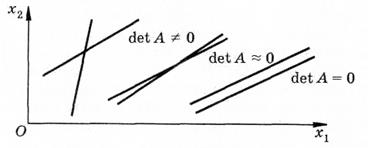
Рисунок 2 – Графическая интерпретация решения системы линейных уравнений

Системы такого типа, в которых есть малые погрешности в коэффициентах системы или в правых частях (эти погрешности могут быть, в частности, результатом округлений при вычислениях или записи чисел в память компьютера), называются ПЛОХО ОБУСЛОВЛЕННЫМИ.

Плохо обусловленная система геометрически соответствует почти параллельным прямым. В теоретических исследованиях обусловленность характеризуется числом обусловленности 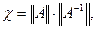при любой норме 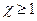. Чем больше это число, тем хуже обусловленность системы; так, при 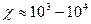система уже плохо обусловлена. На практике, однако, ограничиваются проверкой условия .

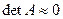Системы линейных уравнений можно было бы рассматривать как частный случай нелинейных уравнений. Однако относительная простота линейных систем обусловила появления специальных высоко эффектных методов их решения. По этой же причине введение и пояснение основных понятий могут быть выполнены относительно просто. Вместе с тем линейные системы представляют собой большой самостоятельный интерес по двум причинам. Во-первых, к системам линейных уравнений приводят многие практические задачи. Во-вторых, важным и неиссякаемым источником систем линейных алгебраических уравнений являются практически все разделы вычислительной математики: нахождение решения системы линейных алгебраических уравнений необходимо в задачах уточнения корней систем нелинейных уравнений, аппроксимации функций, отыскание собственных значений и собственных векторов матрицы, решение обыкновенных дифференциальных уравнений, уравнений в частных производных и т. д. Методы решения линейных уравнений и метод прогонки используются и для некоторых классов интегральных уравнений и интегро-дифференциальных уравнений.

Рассмотрим наиболее употребительные прямые и итерационные методы. ПРЯМЫЕ МЕТОДЫ дают решение задачи за конечное (точно определяемое для каждого метода) число операций. Здесь намеренно не употребляется термин “точные методы”, так как из-за ошибок округления при вычислениях с конечным числом знаков решение всегда получается с погрешностями. Причины этого и способы уменьшения влияния ошибок округления будут обсуждены ниже. Из прямых методов будут рассмотрены метод Гаусса, метод Гаусса с выбором главного элемента для системы линейных алгебраических уравнений общего вида и метод прогонки для систем линейных уравнений с трехдиагональной матрицей.

ИТЕРАЦИОННЫЕ МЕТОДЫ дают решение как предел бесконечной последовательности приближенных решений, в которых каждое последующее более точное приближение находится по уже найденному предыдущему решению (или предыдущим решениям). Из итерационных методов решения систем линейных алгебраических уравнений рассмотрены метод простой итерации и метод Зейделя.