Метод половинного деления. Пусть действительный корень уравнения f(x) = 0 отделен и функция f(x) непрерывна на интервале [a, b] отделения корня

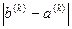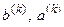Пусть действительный корень уравнения f(x) = 0 отделен и функция f(x) непрерывна на интервале [a, b] отделения корня. Построим процесс сужения интервала [a, b] так, чтобы искомый корень всегда находился внутри суженного интервала. Очевидно, что в этом случае погрешность приближенного значения корня не превышает , где - граничные точки интервала на k-й итерации. Найдем середину отрезка 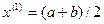и вычислим Составим произведения 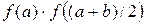и . Из двух половин отрезков выберем тот, в котором произведение является отрицательной величиной, и обозначим новые границы отрезка через 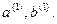Затем новый отрезок разделим пополам, вновь составим аналогичные произведения и выберем тот из отрезков, в котором произведение – величина отрицательная.

Погрешность метода половинного деления, который также называется МЕТОДОМ ДИХОТОМИИ, определяется достаточно очевидным соотношением (которое, впрочем, может быть строго доказано) –

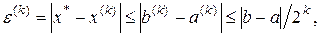
которое указывает на скорость сходимости метода: с увеличением k погрешность стремится к нулю не медленнее геометрической прогрессии со знаменателем . Метод дихотомии прост и надежен, всегда сходится, хотя и медленно, устойчив к ошибкам округления. Метод дихотомии, однако, не обращается на системы уравнений.