Решение нелинейных уравнений

Пусть имеется нелинейное уравнение

f(x)=0 (3.1)

Требуется найти корни этого уравнения, т. е. те значения х, которые обращают уравнение (3.1) в тождество. В процессе приближенного отыскания корней уравнения (3.1) обычно выделяют два этапа: отделение корня и уточнение корня.

Под отделением корня понимается определение промежутка, содержащего один и только один корень уравнения. Одна из точек этого промежутка принимается за начальное приближения корня. В зависимости от метода, который предполагается использовать для уточнения корня, требуется определение тех или иных свойств отделенного корня и поведение функции на отрезке отделения. Например, при использовании простейшего метода уточнения корня – метода дихотомии, необходимо и достаточно установить лишь непрерывность функции на отрезке отделения. При использовании других методов может потребоваться выяснить, является ли корень действительным, какова кратность корня, установить непрерывность и монотонность функции и ее некоторых низших производных.

В общем случае этап отделения корня уравнения (3.1) не может быть алгоритмизирован. Для некоторых классов уравнений (наиболее известным из которых является класс алгебраических уравнений) разработаны специальные приемы отделения корней, существенно облегчающие такое отделение и позволяющее автоматизировать этот процесс. Некоторые из этих приемов будут приведены при рассмотрении методов решений алгебраических уравнений. Нередко отделение корней нелинейных уравнений выполняется “вручную” с использованием всей возможной информации о функции f(x). В ряде случаев приближенное значение корня может быть определенно из физических соображений, если речь идет о решении нелинейного уравнения, связанного с конкретной прикладной задачей. Успешно применяется графический метод определения действительных корней, обладающей большой наглядностью и позволяющий относительно просто устанавливать возможность существования кратных корней. При графическом отделении корней бывает полезным представить уравнение (3.1) в эквивалентном виде 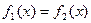и искать точки пересечения функций 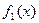и . Например, для уравнения 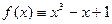вместо построения графика y = f(x) (рис. 3,а) проще построить графики функций и 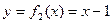(рис.3,б).

В ряде случаев может быть полезной теорема, известная из курса математического анализа.

ТЕОРЕМА. Если функция f(x), определяющая уравнение f(x) = 0 , на концах отрезка 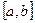принимает значения разных знаков, т. е. 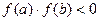, то на этом отрезке содержится по крайней мере один корень уравнения. Если же функция f(x) непрерывна и дифференцируема и ее производная сохраняет знак внутри отрезка 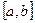, то на этом отрезке находится только один корень 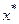уравнения.

Рисунок 3 – Графическое решение уравнения:

а) Пересечение исходной функции и оси абсцисс;

б) Пересечение двух упрощенных функций

В случае, когда на концах интервала функция имеет одинаковые знаки, на этом интервале корни либо отсутствуют, либо их четное число.

Известно, что интервал, на котором расположены корни 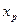многочлена n-й степени 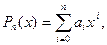в том числе и комплексные, выражается соотношением

.

Кроме того, по правилу знаков Декарта разность между числом перемен знаков последовательности 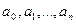и числом положительных корней является либо положительным числом, либо нулем (в случае действительных корней). Это правило распространяется и на отрицательные корни при замене х на –х. Правило Декарта позволяет также оценить число действительных корней на интервале 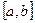. Для этого обозначим и применим правило знаков к уравнению

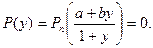
Для отделения корня полезно также использовать теорему Гюа.

ТЕОРЕМА ГЮА. Если все корни алгебраического уравнения являются действительными числами, то для последовательности коэффициентов 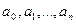квадрат каждого некрайнего коэффициента больше произведения соседних с ним коэффициентов, т. е. 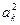> , k = 1, 2, …, n-1.

ТЕОРЕМА. Если для каких-либо k выполнено неравенство то многочлен имеет по крайней мере пару комплексных корней.

На втором этапе уточнения при нахождении корня используют два типа метода: ПРЯМЫЕ и ИТЕРАЦИОННЫЕ. В прямых методах корень уравнения может быть найден за конечное, заранее известное число операций. Прямыми методами удается решить некоторые простейшие алгебраические и тригонометрические уравнения.

В итерационных методах корень 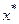определяется как предел некоторой последовательности и решение не может быть достигнуто за конечное, заранее известное число операций.

Основные методы решения нелинейных уравнений и систем являются итерационными, и к их числу принадлежат метод дихотомии (половинного деления), метод простой итерации, метод Ньютона (метод касательных), метод секущих, метод парабол (метод Мюллера), метод Зейделя. Далее эти методы будут рассмотрены.

Важной характеристикой итерационных методов является скорость сходимости процесса. Говорят, что метод имеет n-й порядок сходимости, если , где С - постоянная, не зависящая от n. При n = 1 имеет место сходимость первого порядка, или линейная сходимость, а при n= 2 – второго порядка, или квадратичная. Говорят, что метод является одношаговым, если для построения итерационной последовательности нужно вычислить функцию в одной точке, двушаговым – в двух и т. п.

Сравнение различных методов следует проводить по числу операций при реализации одной итерации и по скорости сходимости.

Изложенные методы решения нелинейных уравнений и систем широко используются в численных методах оптимизации.