Метод исключения Гаусса. Вычисление определителя и обратной матрицы методом исключения

Систему уравнений (2.1) представим в виде

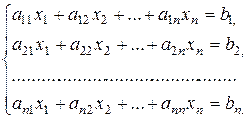(2.3)

или

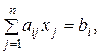i = 1,…, n.

Известно большое число схем метода исключения, приспособленных для ручного или машинного счета матриц общего или специального вида.

Метод Гаусса можно интерпретировать как метод, в котором первоначально матрица приводится к верхней треугольной форме (прямой ход), а далее – к единичной (обратный ход). Очевидно, что если матрица единичная, то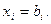

Пусть матрица система (2.3) – верхняя треугольная, поэтому 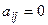при i > j, т. е. все элементы ниже главной диагонали равны нулю. Тогда из последнего уравнения сразу определяем 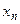. Подставляя 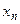в предпоследнее уравнение, находим 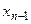и т. д.

Общие формулы имеют вид

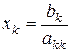при k = n (2.4)

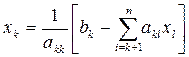при k = n – 1, n – 2, …, 1.

При k > l коэффициенты .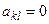

Приведем матрицу системы (2.3) к верхней треугольной. Вычтем из второго уравнения системы (2.3) первое, умноженное на такое число, при котором коэффициент при 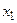обратится в нуль. То же проделаем со всеми остальными уравнениями. В результате все коэффициенты первого столбца, лежащие ниже главной диагонали, обратятся в нуль. Затем, используя второе уравнение, обратим в нуль соответствующие коэффициенты второго столбца. Последовательно продолжая этот процесс, приведем матрицу систему к верхней треугольной форме.

Запишем общие формулы метода Гаусса. Пусть проведено исключение коэффициентов из (k-1)-го столбца. Тогда останутся уравнения с ненулевыми элементами ниже главной диагонали:

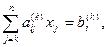
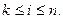
Умножим k-ю строку на число 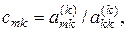m > k и вычтем из m-й строки. Первый ненулевой элемент этой строки обратится в нуль, а остальные изменятся по формулам

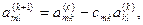
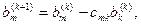k < m.

Проведя вычисления по этим формулам при всех указанных индексах, обратим в нуль элементы k-го столбца, лежащие ниже главной диагонали. Аналогичная процедура приводит матрицу системы к верхней треугольной форме, при этом весь процесс приведения называется ПРЯМЫМ ХОДОМ МЕТОДА ГАУССА. Вычисление неизвестных по формулам (2.4) называют ОБРАТНЫМ ХОДОМ метода.

Обратный ход можно совершить иначе, если обратить в нуль и все коэффициенты, лежащие выше главной диагонали. Например, элементы n-го столбца обращаются в нуль, если 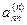умножить на 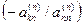и сложить с соответствующей строкой. Аналогично обращаются в нуль и все остальные столбцы. Если, кроме того, разделить затем каждое уравнение на соответствующий элемент, стоящий на главной диагонали, то матрица системы становится единичной, а неизвестны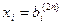е , где 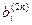- коэффициенты правой части i-го уравнения после указанных преобразований.

На некотором шаге прямого хода может оказаться, что коэффициент 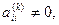но мал по сравнению с остальными элементами матрицы системы и, в частности, мал по сравнению с элементами первого столбца. Деление коэффициентов системы на малую величину может привести к значительным ошибкам округления.

Для уменьшения ошибок округления поступают следующим образом. Среди элементов первого столбца 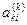каждой промежуточной матрицы выбирают наибольший по модулю (главной) элемент и путем перестановки i-го строки со строкой, содержащей главный элемент, добиваются того, что главный элемент становится ведущим. Такая модификация метода исключения Гаусса называется методом Гаусса с выбором главного элемента. Случай появления нулевых элементов обходится при этом сам собой.

Для реализации метода требуется примерно 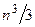операций типа умножения и 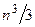операций типа сложения. Полезно помнить, что оценка числа операций определяется в основном операциями, затрачиваемыми при выполнении прямого хода метода Гаусса. Обратный ход метода Гаусса требует примерно 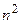операций.