Численные методы решения линейных уравнений
Метод прогонки
Системы линейных уравнений с трехдиагональной матрицей коэффициентов при неизвестных являются наиболее важным и распространенным случаем систем специального вида. В таких системах отличны от нуля только элементы, лежащие на главной диагонали и на нижней и верхней диагоналях, прилегающих к ней. К системам с трехдиагональными матрицами приводят, например, задачи о сплайн-интерполяции, о решении разностными методами обыкновенных дифференциальных уравнений и уравнений в частных производных.
Метод прогонки принадлежит к числу прямых методов решения систем линейных уравнений и используется в тех случаях, в которых многие коэффициенты матрицы равны нулю. Это обстоятельство учтено при реализации метода прогонки, в котором исключаются преобразования с нулевыми элементами. В методе прогонки применительно к системе линейных уравнений, имеющих трехдиагональную матрицу, можно выделить следующие этапы.
• Приведение трехдиагональной матрицы к верхней треугольной (прямой ход), В случае трехдиагональной матрицы это означает приведение к двухдиагональной, т. е. приведение исходной системы к системе, содержащей по два неизвестных в каждом уравнении, кроме последнего, в котором содержится только одно неизвестное.
• Запись обратного хода в виде 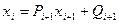 , так как преобразованная матрица – двухдиагональная.
, так как преобразованная матрица – двухдиагональная.
•Вывод рекуррентного соотношения для 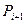 и
и 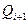 через
через 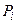 и
и  и получение соотношения для
и получение соотношения для 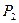 и
и 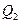
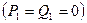 .
.
• Осуществление обратного хода метода прогонки и определение всех неизвестных.
Рассматриваемый метод прогонки представляет собой модификацию метода исключения Гаусса, использующую специальный регулярный вид матрицы системы. Запишем систему линейных алгебраических уравнений с трехдиагональной матрицей в виде
 i = 1,2,…, n, (2.6)
i = 1,2,…, n, (2.6)
Запись (2.6) представляет собой так называемый КАНОНИЧЕСКИЙ ВИД СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДА ПРОГОНКИ. При этом матрица система (2.6) имеет вид

Прямой ход метода прогонки сводится к исключению неизвестного 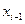 в каждом уравнении системы. Получаемая в результате прямого хода система содержит в каждом уравнении только два неизвестных
в каждом уравнении системы. Получаемая в результате прямого хода система содержит в каждом уравнении только два неизвестных 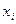 и
и 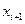 , и матрица ее – верхняя треугольная с двумя диагоналями. Запишем i-ю строку преобразованной двухдиагональной матрицы в виде
, и матрица ее – верхняя треугольная с двумя диагоналями. Запишем i-ю строку преобразованной двухдиагональной матрицы в виде
 (2.7)
(2.7)
Если система (2.6) приведена к виду (2.7), то обратный ход метода Гаусса очевиден. Однако использование общих алгоритмов прямого и обратного хода нецелесообразно. Построим эффективную вычислительную схему, которая и составляет суть метода прогонки. Для этого, уменьшив в (2.7) индекс на единицу, запишем

Подставляя 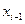 в систему (2.6), получим соотношение
в систему (2.6), получим соотношение
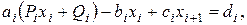
из которого нетрудно получить

Сравнивая это соотношение с (2.7), можем записать рекуррентные соотношения
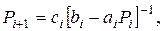
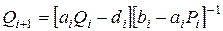 (2.8)
(2.8)
для вычисления так называемых ПРОГОНОЧНЫХ КОЭФФИЦИЕНТОВ.
Подчеркнем, что последующие значения прогоночных коэффициентов 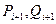 вычисляются только по известным коэффициентам системы (2.6) и известным предыдущим значениям прогоночных коэффициентов
вычисляются только по известным коэффициентам системы (2.6) и известным предыдущим значениям прогоночных коэффициентов 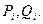
Для начала прямого хода метода прогонки необходимо задать начальные (стартовые) значения прогоночных коэффициентов, например, 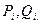 Отметим, что, вообще говоря, начальные значения коэффициентов
Отметим, что, вообще говоря, начальные значения коэффициентов 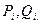 в рассмотренной схеме вычислений не требуются, так как значения коэффициентов
в рассмотренной схеме вычислений не требуются, так как значения коэффициентов  вычисляются только через коэффициенты первого уравнения системы (2.6): при i = 1 из (2.6) получаем соотношение
вычисляются только через коэффициенты первого уравнения системы (2.6): при i = 1 из (2.6) получаем соотношение 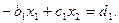 Сравнивая это выражение с (2.7) при i =1, получаем
Сравнивая это выражение с (2.7) при i =1, получаем 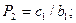
 а значение
а значение  в обратном ходе вычисляем по соотношению
в обратном ходе вычисляем по соотношению 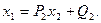 Использование
Использование 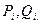 в качестве начальных значений целесообразно по двум причинам: сохраняется однородность вычислительного алгоритма для всех i = 2, 3, …,n; упрощается обсуждение и доказательство условия корректности и устойчивости метода прогонки. Из того обстоятельства, что коэффициенты
в качестве начальных значений целесообразно по двум причинам: сохраняется однородность вычислительного алгоритма для всех i = 2, 3, …,n; упрощается обсуждение и доказательство условия корректности и устойчивости метода прогонки. Из того обстоятельства, что коэффициенты  не зависят от
не зависят от 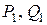 (в соотношениях(2.8) при i =1 коэффициенты
(в соотношениях(2.8) при i =1 коэффициенты 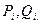 умножаются на
умножаются на  ), следует, что можно задать любые значения для прогоночных коэффициентов
), следует, что можно задать любые значения для прогоночных коэффициентов 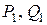 . Далее будет ясно, почему удобно положить
. Далее будет ясно, почему удобно положить 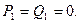 Для начала обратного хода метода прогонки необходимо для вычисления
Для начала обратного хода метода прогонки необходимо для вычисления 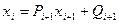 задать значение
задать значение  . Так как
. Так как 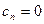 , то из первого соотношения (2.8) вытекает, что
, то из первого соотношения (2.8) вытекает, что 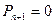 и, следовательно, можно задать любое значение для
и, следовательно, можно задать любое значение для 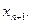 Обычно полагают
Обычно полагают 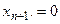 , и тогда
, и тогда 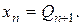
Метод прогонки устойчив, если 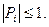 Метод прогонки корректен, если
Метод прогонки корректен, если 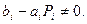
Отметим, что при устойчивости метода прогонки ошибки округления не возрастают, а подавляются. Пусть 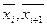 - вычисленные с погрешностями значения решения. Пусть при этом коэффициенты
- вычисленные с погрешностями значения решения. Пусть при этом коэффициенты 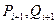 вычисляются точно. Тогда по (2.7)
вычисляются точно. Тогда по (2.7)
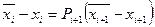
или
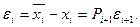
Из этой формулы при  следует, что в данном случае погрешность не возрастает.
следует, что в данном случае погрешность не возрастает.
Достаточным условием корректности метода прогонки и устойчивости его к погрешностям является условие преобладания диагональных коэффициентов:
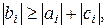 i = 1,2, …, n.
i = 1,2, …, n.
В самом деле, если хотя бы для одного значения i выполняется строгое неравенство  , то можно записать цепочку неравенств:
, то можно записать цепочку неравенств:
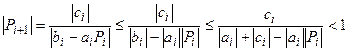 .
.
Было показано, что можно положить 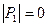 и тогда, во-первых, для всех i выполняется
и тогда, во-первых, для всех i выполняется 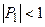 , что обеспечивает затухание погрешности, и, во-вторых, для всех i выполняется условие
, что обеспечивает затухание погрешности, и, во-вторых, для всех i выполняется условие 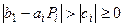 и, таким образом, не возникает ситуация деления на нуль. Так как условие
и, таким образом, не возникает ситуация деления на нуль. Так как условие 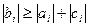 является только достаточным, то невыполнение его не означает нарушения корректности и устойчивости.
является только достаточным, то невыполнение его не означает нарушения корректности и устойчивости.
Для реализации метода требуется примерно 8n операций, из которых 3n составляют операции типа умножения и 5n – операции типа сложения. При численном решении дифференциальных уравнений используются различные варианты метода прогонки: метод встречных прогонок, потоковая прогонка, матричная прогонка для систем векторных уравнений. Отметим, что
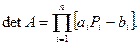
Метод прогонки обобщается на случай, при котором в системе (2.6) 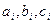 - квадратные матрицы размерности
- квадратные матрицы размерности 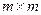 , а
, а 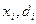 - векторы размерности m. Тогда соотношения (2.7) и (2.8) метода прогонки, в которых все действия совершаются уже над матрицами, а не над скалярами, сохраняются, а
- векторы размерности m. Тогда соотношения (2.7) и (2.8) метода прогонки, в которых все действия совершаются уже над матрицами, а не над скалярами, сохраняются, а 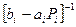 в (2.8) является соответствующей обратной матрицей.
в (2.8) является соответствующей обратной матрицей.
Условие устойчивости матричной прогонки выглядит как 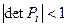 , а условие корректности и устойчивости имеет вид
, а условие корректности и устойчивости имеет вид  .
.
Дата добавления: 2015-11-06; просмотров: 3910;
