Метод простой итерации

При использовании метода простой итерации для уточнения корня уравнение f(x) = 0 заменяется эквивалентным уравнением

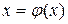(3.2)

Это означает, что из 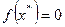следует 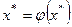и наоборот. Привести уравнение (3.1) к уравнению (3.2) можно многими способами, например, положив 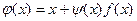, где 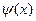- непрерывная произвольная знакопостоянная функция.

Геометрически на интервале отделения корня уравнение (3.2) представляется в виде двух пересекающихся линий 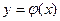и y = x (рис. 4). Пологая, что известно начальное приближение 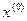для значения корня 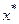, построим итерационный процесс

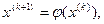k = 0, 1, 2, …, (3.3)

изображенный на рис.4 ломаной линией со стрелочками, указывающими направление движения. Для представленного на рис.4 случая взаимного расположения линий y = x и 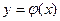неограниченное повторение вычислений по соотношению (3.3) позволяет сколь угодно близко подойти к точному значению корня .

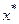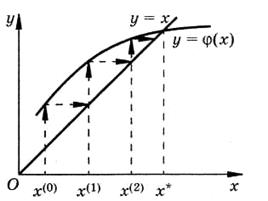
Рисунок 4 – Геометрическая интерпретация метода простой итерации

Исследуем сходимость метода. Если 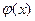имеет непрерывную производную, то из теоремы Лагранжа о конечном приращении

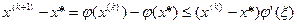(3.4)

следует, что точка 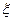лежит между точкам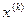и и 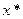. Поэтому если всюду 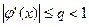, то отрезки 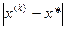убывают не медленнее геометрической прогрессии со знаменателем q<1. Действительно, из (3.4), которое можно рассматривать как рекуррентное соотношение, следует, что 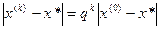и последовательность 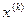сходится при любом нулевом приближении.

Итак, условие

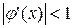(3.5)

Является достаточным условием сходимости итераций. Если 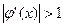, то итерации могут не сходиться. Если 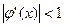, но вдали от корня 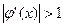, то итерации сходятся, если начальное приближение выбрано достаточно близко к корню. При произвольном начальном приближении сходимости может не быть. Таким образом, в методе простой итерации важен выбор начального приближения. Из соотношения (3.4) следует, что если на интервале отделения корня выполняется условие

,

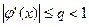то погрешность на каждой итерации уменьшается для любого начального приближения не медленнее членов геометрической прогрессии со знаменателем q.

Четыре случая взаимного расположения линий y = x и 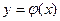вблизи корня и соответствующие им итерационные процессы показаны на рис. 5, a и 5. б соответствуют случаю 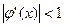– процесс итераций сходится. При этом в первом случае 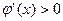и сходимость носит односторонний характер (рис. 5, а), а во втором 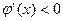и сходимость носит двусторонний характер (рис. 5, б). Рис. 5, в и 5, г соответствуют случаю 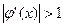– процесс итерации расходится, при этом имеет место односторонняя и двусторонняя расходимость.

Подчеркнем, что условие (3.5) сходимости метода итераций является лишь достаточным. При этом все приближения должны попадать в отрезок отделения корня. Выполнение условия (3.5) гарантирует сходимость процесса (3.3), но невыполнение условия (3.5) в общем случае не означает, что итерационный процесс окажется расходящимся. Например, для случая, проиллюстрированного рис.6, условие (3.5) на интервале 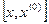не выполняется, но метод итераций сходится.

Используя соотношения(3.4) и (3.5), можно записать

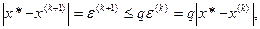
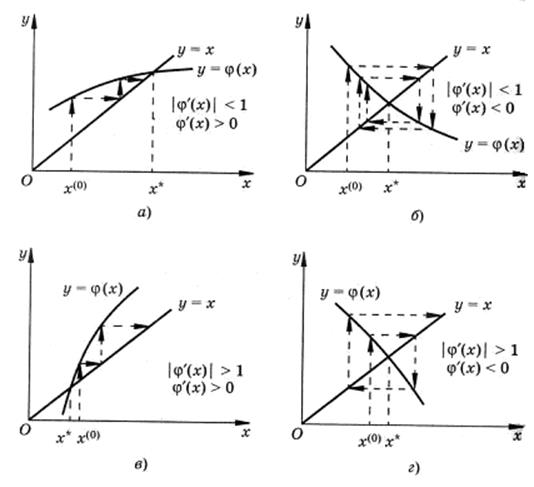
Рисунок 5 – Типовые случаи устойчивой и неустойчивой реализации метода простой итерации

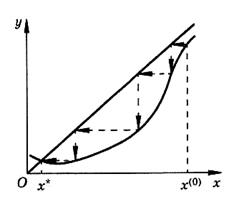
Рисунок 6 – Частный случай сходимости метода простой итерации

где 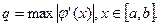Из этого соотношения следует, что скорость сходимости метода итерации зависит от величины q: чем меньше q, тем быстрее сходится метод.

Исходное уравнение f(x) = 0 может быть преобразовано к виду 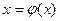многими способами, и, очевидно, для метода итерации целесообразно брать то уравнение 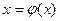, для которого q имеет наименьшее значение.

Для пояснения рассмотрим классический пример вычисления квадратного корня. Исходное уравнение 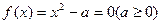преобразуем к виду 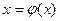тремя способами, приведенными в табл. 1 в первом столбце.

Анализ поведения 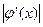вблизи корня (третий столбец таблицы) показывает, что при удачном выборе представления 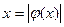можно обеспечить высокую скорость сходимости итерационного процесса без ограничения диапазона параметра а. Третье уравнение 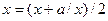используется для вычисления квадратного корня на компьютерах. Таким образом, в методе простой итерации важен выбор вида функций 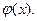Отметим, что метод простой итерации обобщается на случай систем линейных уравнений.

Таблица 1. Примеры выбора функции 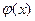в методе простой итерации

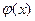
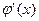
		Поведение	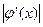Сходимость метода
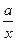
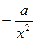
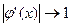		при	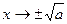Не сходится
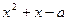
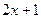
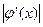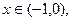
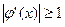		<1 при при	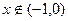Сходится в ограниченном интервале к отрицательному значению корня
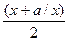
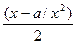
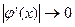		при	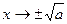Сходится, и очень быстро

Метод Ньютона

Вновь рассмотрим уравнение (3.1). Полагая, что погрешность 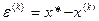мала, а функция f(x) имеет непрерывную вторую производную, разложим 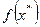в ряд Тейлора:

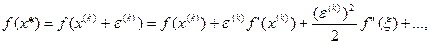
где 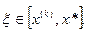. Учитывая, что 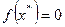и оставляя только линейную часть разложения в ряд (отсюда и другое название метода – МЕТОД ЛИНЕАРИЗАЦИИ), можем записать приближенное, линейное относительно погрешности, уравнение

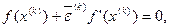
из которого для погрешности имеем

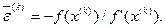(3.6)

Так как использована лишь линейная часть разложения в ряд, то при подстановке (3.6) в соотношение 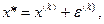следующее из соотношения для погрешности, получим вместо 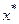лишь приближенное уточненное значение корня, которое обозначим 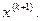Тогда можем записать основное соотношение метода Ньютона в виде

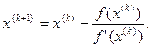(3.7)

Это соотношение позволяет построить последовательность приближений 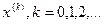к точному значению корня по заданному приближению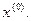

Геометрически процесс (3.7) означает замену на каждой итерации кривой y = f(x) на касательную к ней в точке 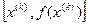и определение значения 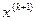как координаты точки пересечения касательной и оси абсцисс (рис. 7). С рассмотренной интерпретацией соотношения (3.7) связано еще одно название метода – МЕТОД КАСАТЕЛЬНЫХ.

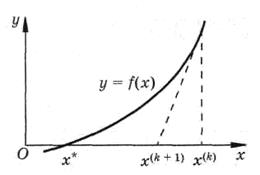
Рисунок 7 – Геометрическая интерпретация метода Ньютона

Достаточное условие сходимости метода Ньютона получим из соответствующего условия для метода простой итерации. Сопоставляя соотношения (3.2) и (3.7), можно заключить, что метод простой итерации, в котором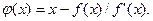

Используя условие сходимости метода итераций 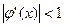и выражение

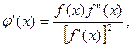
Нетрудно получить достаточное условие сходимости метода Ньютона в форме

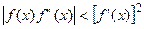. (3.8)

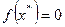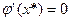Поскольку , то , и итерации по соотношению (3.7) сходятся к точному значению корня при произвольном начальном приближении, но вдали от корня сходимость может быть немонотонной.

Для оценки скорости сходимости метода Ньютона запишем соотношение

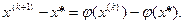
Далее разложим 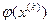в ряд Тейлора:

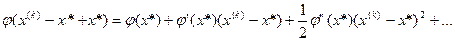
Подставляя это разложение в предыдущую формулу, и учитывая, что 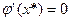, получаем

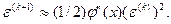
Из этого соотношения следует, что метод Ньютона имеет вблизи корня второй порядок сходимости: на каждой итерации ошибка меняется пропорционально квадрату ошибки на предыдущей итерации. Нетрудно видеть, что метод Ньютона является одношаговым. Достоинства метода Ньютона состоят в его квадратичной сходимости, возможности обобщения на случай систем уравнений, а также в том, что он является одношаговым. Однако метод Ньютона расходится в тех областях, где 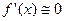. Кроме того, если функция f(x) задана таблично, то вычисление 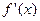затруднено. Указанная трудность устраняется в методе секущих (методе хорд).

Существует вариант метода Ньютона с постоянным значением производной; значение производной вычисляется только в начальной точке 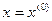(рис. 8), и далее для всех итераций значения производных 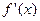полагаются постоянными, равными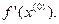

Последовательные приближения вычисляются по формуле

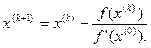
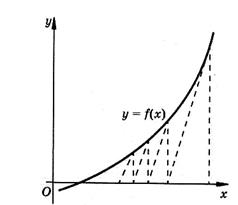
Рисунок 8 – Модифицированный метод Ньютона

Геометрически замена производной на каждой итерации постоянным значением означает, что наклон прямой, точка пересечения которой с осью абсцисс принимается за новое приближение для корня уравнения, считается постоянным. Часто эта модификация метода Ньютона рекомендуется, как позволяющая уменьшить объем вычислений за счет отказа от вычисления производной на каждой итерации. Однако следует учитывать, что метод Ньютона с постоянным значением производной имеет лишь первый порядок сходимости – вблизи корня соотношение для погрешности имеет вид

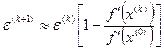
и, следовательно, сходится медленнее, чем метод Ньютона. Это, в конечном счете, нередко приводит к увеличению общего объема вычислений.

Метод секущих

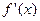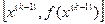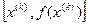В методе секущих, иначе называемом МЕТОДЕ ХОРД, приближенное значение производной в формуле (3.7) определяется по двум последовательным приближениям и по соотношению

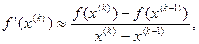(3.9)

что приводит к замене касательной в точке 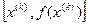секущей, проведенной через две точки кривой y = f(x) (рис.9) или, что то же самое, - к аппроксимации функции f(x) на этом интервале линейной функцией.

Условия сходимости метода секущих аналогичны условиям сходимости метода Ньютона. Порядок сходимости метода секущих определяется соотношениями

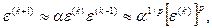
где .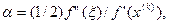

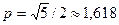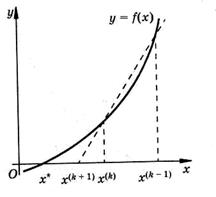
Рисунок 9 – Геометрическая интерпретация метода секущих

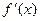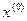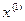К особенностям метода следует отнести следующее: в методе не требуется непосредственного вычисления производной на каждой итерации, которое может привести к существенному уменьшению объема вычислений; метод является двухшаговым, и, в частности, на первой итерации вычислений необходимо знать два начальных значения и ; сходимости метода может быть немонотонной даже в малой окрестности корня; в знаменателе формулы для вычисления 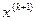стоит разность двух величин 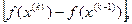которые имеют вблизи корня малые и близкие значения, что может привести к заметным погрешностям вычислений, особенно для кратных корней.

Метод парабол

Рассмотренный метод секущих можно интерпретировать как метод, в котором на каждой итерации исходная функция аппроксимируется линейной функцией (секущей), построенной по двум точкам, принадлежащим f(x). Развивая далее идеи аппроксимации, можно для построения итерационных формул использовать информацию о функции в нескольких точках, предшествующих точке 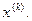В методе парабол по трем последовательным приближениям 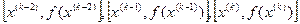строится многочлен второй степени (парабола), приближающий исходную функцию. Иначе этот метод называют МЕТОДОМ МЮЛЛЕРА или методом КВАДРАТИЧНОЙ ИНТЕРПОЛЯЦИИ. За новое приближение берется обычно ближайший к 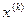корень соответствующего квадратного уравнения. Геометрическая интерпретация метода парабол дана на рис.10.

В качестве 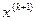выбирается тот из корней квадратного уравнения, для которого величина 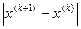наименьшая. Доказывается, что погрешность метода определяется соотношением

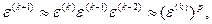
где p = 1,839.

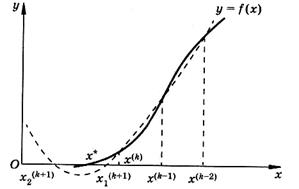
Рисунок 10 – Геометрическая интерпретация метода парабол

Это означает, что, несмотря на привлечение дополнительной информации о функции, метод парабол имеет порядок сходимости, лишь немного превышающий порядок сходимости метода секущих. Вместе с тем возникают задачи решения квадратного уравнения, выбора одного из двух корней многочлена и, самое важное, определение области гарантированной сходимости метода. Если три приближения для построения многочлена выбраны далеко от корня и содержат погрешности, то возможно самое неожиданное поведение решения.

Отметим, что метод парабол успешно применяется для отыскания корней многочленов, в том числе комплексных; при этом метод обладает тем замечательным свойством, что начальное приближение может быть действительным. Метод парабол является трехшаговым методом.