Функция и способы ее задания

Из курса математического анализа известны 3 способа задания функциональных зависимостей: аналитический, графический и табличный.

Наиболее удобным способом задания функциональной зависимости 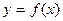является аналитический, так как он прямо указывает действие и последовательность их выполнения над независимой переменной х для получения соответствующего значения. Например, путь и время при равноускоренном движении связаны соотношением 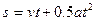. Преимуществом данного способа является возможность получать значения у для любого фиксированного аргумента х с любой точностью. К недостаткам следует отнести то, что приходится производить всю последовательность вычислений, кроме того, аналитический метод не обладает наглядностью.

Указанные недостатки аналитического способа устраняются в случае графического способа задания функции у = f(x).

Табличный способ задания функции распространен в технике, физике, экономике, естествознании (и чаще всего возникает в результате эксперимента). Преимуществом этого способа является то, что для каждого значения независимой переменной, помещенной в таблицу можно без всяких измерений и вычислений, найти соответствующее значение функции. Недостаток состоит, что нельзя задать всю функцию, т.е. всегда найдутся такие значения независимой переменной, которых нет в таблице.

Основные понятия теории приближения функций

Теорией и практикой приближения (аппроксимации) функции приходится пользоваться при решении многих практических задач.

Например, в процессе некоторого эксперимента в дискретные моменты времени 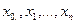получены значения 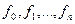некоторой величины f(x). Требуется восстановить функцию f(x) при других 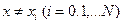. Подобная же задача возникает при многократном вычислении на ЭВМ одной и той же сложной функции f в различных точках. Вместо этого часто бывает целесообразно вычислить функцию f в небольшом числе характерных точек 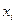, а в остальных точках найти ее значение по некоторому более простому правилу, используя информацию об уже известных значениях .

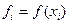Другими распространенными примерами аппроксимации функций являются задачи определения производной 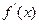и интеграла 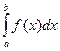по заданным значениям .

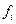Наконец при составлении алгоритмов стандартных программ для вычисления элементарных и специальных функций снова возникает задача приближение функций.

Классический подход к решению подобных задач заключается в том, чтобы, используя имеющеюся информацию о функции f, рассмотреть другую функцию 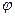, близкую в этом смысле к f и позволяющую выполнить над ней соответствующую операцию и получить оценку погрешности такой «аналитической замены».

В процессе численной реализации этого подхода необходимо рассмотреть следующие четыре основных вопроса:

1. Вопрос об имеющейся информации относительно функции f, т.е. о виде, в котором задана функция f. Различают два основных случая: функция f задана либо аналитически, либо в виде таблицы. Графический способ относят к первому, или ко второму случаю в зависимости от конкретной задачи. В дальнейшем будем рассматривать на отрезке 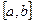непрерывные вместе с достаточным количеством своих производныхфункций f(x),определенные значениями 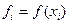в узлах 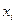заданной сетки .

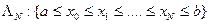2. Вопрос о классе аппроксимирующих функций, т.е. какими функциями 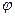будет аппроксимирована функция f. Во-первых, аппроксимирующая функция должна отражать характерные особенности аппроксимируемой, а во-вторых, быть достаточно удобной в обращении, т.е. при выполнении над ней необходимых операций.

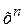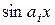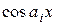В численном анализе широкое применение имеют 3 группы аппроксимирующих функций. Первая – функции вида 1, х, …, , линейные комбинации которых порождают класс всех много членов степени не выше n. Вторую группу образуют тригонометрические функции и , порождающие ряды Фурье, и интеграл Фурье. Третья группа состоит из экспоненциальных функций 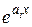, определяющих явления типа распада и накопления, часто встречающихся в реальных ситуациях.

Принимаем в качестве аппроксимирующей функции многочлен некоторой степени n. В этом случае функция имеет вид .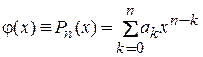

3. Вопрос о близости аппроксимируемой и аппроксимирующей функций, т.е. о выборе критерия согласия, которому должна удовлетворять функция .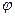

Одним из распространенных критериев согласия является критерий Чебышева, основанный на понятии расстояния как максимальной величины отклонения функции f в узлах .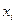

.

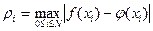Наибольший интерес представляет частный случай, когда для аппроксимирующей функции расстояние 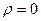. Это означает, что для табулированной функции y=f(x), заданной значениями 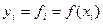(табл. 2) требуется построить аппроксимирующую функцию 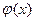, совпадающую в узлах со значениями заданной функции у=f(x), т.е. такую, что .

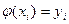Таблица 2. Структура табличного задания функции

		….
		….

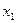
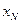
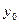
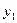
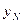
Такой способ аппроксимации, основанный на критерии совпадения f и 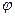в узлах 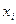, называется интерполированием (или интерполяцией). Если аргумент, для которого определяется приближенное значение функции, принадлежит отрезку 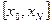, то задача вычисления значение функции в точке х называется интерполированием в узком смысле. Если же аргумент х находятся вне отрезка 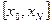, то поставленная задача называется экстраполированием.

Геометрически задача интерполирование для функции одной переменной y=f(x) означает построение на плоскости Х0У кривой, проходящей через точки с координатами .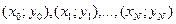

Приведем еще один пример критерия согласия. Введем понятие расстояния между функциями f и 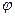как суммы квадратов их отклонений в узловых точках:

.

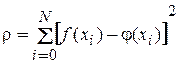Выберем в качестве аппроксимирующей функции ту, для которой 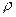минимально. Этот критерий целесообразно использовать в случае большого количества информации, заданной с невысокой точностью. Метод аппроксимации, основанный на данном критерии, называют методом наименьших квадратов. К достоинствам этого метода следует отнести простоту и стройность его математической теории.

4. Вопрос о погрешности, т.е. об определении разности между точным и приближенным значениями. В конечном итоге качество метода определяется быстротой получения решения с требуемой точностью (скоростью сходимости). На первый взгляд вопрос о точности получаемого решения кажется довольно простым: необходимо, чтобы приближенное решение отличалось от точного не более чем на заданное 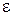. Однако вопрос о возможности сколь угодно точного приближения функции f в общем случае остается открытым и подлежит исследованию для каждого конкретного аппроксимационного процесса.