Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа представляет собой линейную комбинацию
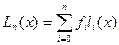 , (4.10)
, (4.10)
где 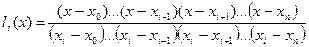 .
.
Выражение (3.10) есть многочлен степени не выше n. В узле 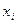 этот многочлен принимает значение
этот многочлен принимает значение 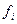 , так как
, так как
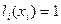 (i=0,1,…,n);
(i=0,1,…,n);
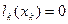
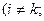
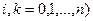 .
.
Учитывая, что
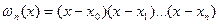 ,
,
Можно рассмотреть его производную в точке 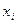 :
:
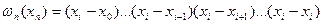
и записать многочлен Лагранжа в виде
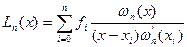 .
.
Величины 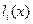 являются как бы весовыми многочленами соответствующих узлов и называются множителями Лагранжа.
являются как бы весовыми многочленами соответствующих узлов и называются множителями Лагранжа.
Интерполяционный многочлен Лагранжа для равноотстоящих узлов интерполяции (т.е. 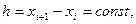 где h – шаг интерполяции) можно записать в виде
где h – шаг интерполяции) можно записать в виде
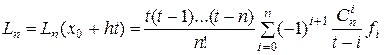 , (4.11)
, (4.11)
где
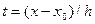 ;
; 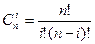 .
.
Пример 2.Функция y=sin(x) задана в виде таблицы (табл.3)
Таблица 3. Данные к примеру 2
| x | 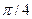
| 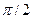
| |
| y | 0.707 |
Пользуясь интерполяционным многочленом Лагранжа, определить ее значение в точке 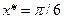 . Оценить погрешность
. Оценить погрешность  .
.
Прежде всего определим 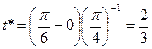 . Подставляя в формулу (4.11) полученное значение
. Подставляя в формулу (4.11) полученное значение 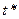 и значение
и значение 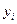 при n=2, имеем
при n=2, имеем
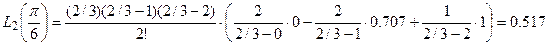
Для оценки погрешности воспользуемся формулой (4.9). Тогда 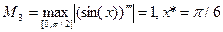 поэтому
поэтому
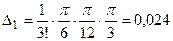 .
.
При вычислении погрешности градусную меру следует перевести в радиальную.
Итак, получили 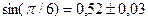 .
.
Конечные разности
При построении интерполяционных многочленов на равномерной сетке используются величины, называемые конечными разностями.
Рассмотрим равномерную сетку с шагом h: 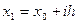
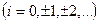 , в узлах которой заданы значения
, в узлах которой заданы значения  функции
функции 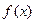 .
.
В математической литературе используются три типа конечных разностей: нисходящие разности 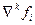 для интерполяции назад; центральные разности
для интерполяции назад; центральные разности 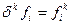 для построения центральных интерполяционных формул и восходящие разности
для построения центральных интерполяционных формул и восходящие разности 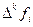 для интерполяций вперед.
для интерполяций вперед.
Конечной разностью первого порядка называется разность между значениями функции в данном и предыдущем узлах:
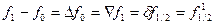
…… (4.12)
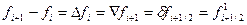
Это определение можно записать в другой форме:
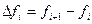 ;
; 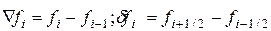 (4.13)
(4.13)
Конечной разностью второго порядка называетсяразность между значениями первой конечной разностью второго в данном и предыдущем узлах:
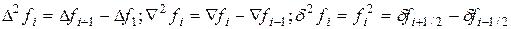 . (4.14)
. (4.14)
Аналогичным образом определяются конечные разности произвольного порядка k:
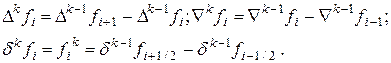 (4.15)
(4.15)
В некоторых рассчитываемых ниже интерполяционных формулах наряду с разностями (4.15) используются средние арифметические соседних конечных разностей одного и того же порядка:
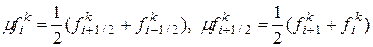 (4.16)
(4.16)
Первая из этих величин используется при нечетном k, а вторая – четном k.
Рассмотрим некоторые свойства конечных разностей.
1. Нисходящие, восходящие и центральные разности связанны между собой следующими соотношениями:
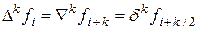 (4.17)
(4.17)
2. Конечная разность удовлетворяет равенству
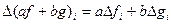 , (4.18)
, (4.18)
где а и b постоянные.
3. Конечная разность связана с соответствующей производной соотношением
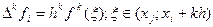 (4.19)
(4.19)
4. Конечная разность порядка k может быть представлена в виде следующей линейной комбинации значений 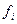 :
:
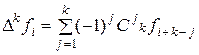 , (4.20)
, (4.20)
где 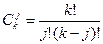 - число сочетаний из к элементов по j элементов (причем
- число сочетаний из к элементов по j элементов (причем  ).
).
Исходные значения функции 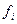 , как правило, задаются с некоторой погрешностью
, как правило, задаются с некоторой погрешностью 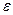 , представляющей собой ошибки округления или случайные ошибки, поэтому целесообразно рассматривать влияние этих факторов на погрешности конечных разностей высших порядков.
, представляющей собой ошибки округления или случайные ошибки, поэтому целесообразно рассматривать влияние этих факторов на погрешности конечных разностей высших порядков.
Если значения 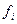 заданы приближенно или же по каким-либо причинам вычисленные значения многочлена
заданы приближенно или же по каким-либо причинам вычисленные значения многочлена 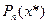 не может быть произведено абсолютно точно, то фактически получается лишь приближенное значение
не может быть произведено абсолютно точно, то фактически получается лишь приближенное значение 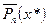 для точного
для точного 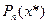 . При этом вычислительная погрешность
. При этом вычислительная погрешность
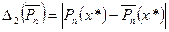
оценивается по общим правилам вычисления погрешности.
Рассмотрим многочлен Лагранжа 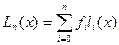 . Пусть требуется вычислить
. Пусть требуется вычислить 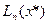 при заданных значениях
при заданных значениях 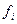 и их погрешностях
и их погрешностях 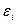 . Величины коэффициентов Лагранжа
. Величины коэффициентов Лагранжа  протабулированы для равностоящих узлов и их можно считать точными числами, поскольку они получены из точных значений узлов и точного х*. Поэтому для многочленов Лагранжа имеем:
протабулированы для равностоящих узлов и их можно считать точными числами, поскольку они получены из точных значений узлов и точного х*. Поэтому для многочленов Лагранжа имеем:
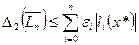 .
.
В случае, когда все 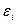 одинаковы и равны
одинаковы и равны 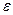 , получаем
, получаем
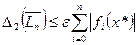 .
.
Пример 3.На отрезке 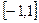 получить равномерную оценку вычислительной погрешности значений интерполяционного многочлена Лагранжа, построенного для функции
получить равномерную оценку вычислительной погрешности значений интерполяционного многочлена Лагранжа, построенного для функции 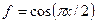 по узлам
по узлам 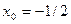 ,
, 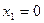 ,
, 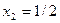 .
.
Так как 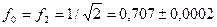 , а
, а 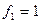 есть точное число, то искомая вычислительная погрешность имеет вид
есть точное число, то искомая вычислительная погрешность имеет вид
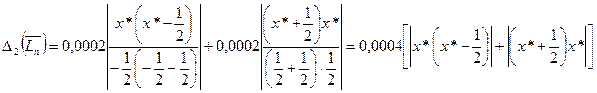
Нетрудно показать, что на данном отрезке 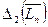 принимает максимальное значение в точках
принимает максимальное значение в точках 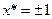 , и по этому искомая оценка есть
, и по этому искомая оценка есть 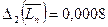 .
.
Дата добавления: 2015-11-06; просмотров: 1569;
