Разделенные разности

Рассмотрим случай, когда значение функции заданы в неравноотстающих узлах. При этом вместо конечных разностей рассматриваются разделенные разности, являющиеся в некотором смысле аналогом понятия производной и определяющиеся следующим образом.

Пусть функция y = f(x) задана своими значениями ,

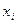, ,…, , … в узлах произвольной сетки .

Разделенные разности нулевого порядка совпадают со значениями функции в точках 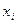. Разделенными разностями первого порядка называются отношения

Разделенными разностями второго порядка называются отношения

В общем случае разделенная разность k-го порядка определяется через разделенную разность(k-1)-го порядка по формуле

. (4.36)

Приведем некоторые свойства разделенных разностей

1. Разделенные разности всех порядков являются линейной комбинацией значений , а именно справедлива следующая формула:

. (4.37)

2. Разделенная разность есть симметрическая функция своих аргументов, т.е. не меняется при любой их перестановке.

3. Разделенная разность удовлетворяет равенству

, (4.38)

4. Если узлы принадлежат отрезку и функция f(x) имеет на непрерывную производную k-го порядка, то существует такая точка , что

. (4.39)

Из этого свойства вытекает простое следствие. Пусть

есть многочлен k-й степени. Тогда, очевидно, , и соотношение (4.39) дает для разделенной разности значение

Итак, у всякого многочлена k-й степени разделенные разности k – го порядка равны постоянной величине – коэффициенту при старшей степени многочлена. Разделенные разности высших порядков (больше k), очевидно, равны нулю.