Итерационно-интерполяционный метод Эйткина

В тех случаях, когда нет необходимости в получении приближенного аналитического выражения функции f(x), заданное таблично, а требуется лишь определить значение этой функции в некоторой точке 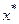, отличной от узлов интерполяции, целесообразно использовать итерационно-интерполяционный метод Эйткина. По существу, этот метод заключается в последовательной линейной интерполяции. Процесс вычисления 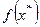состоит в следующем. Пронумеруем узлы интерполяции, например, в порядке удаления их от 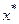и составим матрицу:

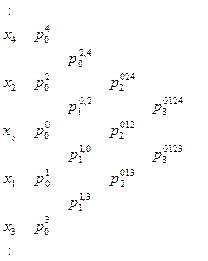
Здесь

;

-

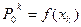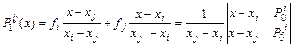интерполяционный многочлен первой степени, построенный по узлам ;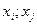

-

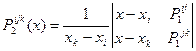интерполяционный многочлен второй степени, построенный по узлам 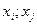; 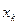. Продолжая этот процесс, построим многочлен

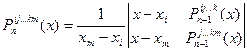. (4.43)

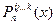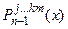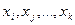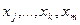Покажем, что если и - интерполяционные многочлены, построенные соответственно по узлам и , то 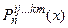- интерполяционный многочлен, построенный соответственно по узлам .

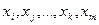Действительно, во-первых, 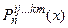- многочлен степени не выше n, что очевидно из построения формулы (4.43). Во-вторых, во всех узлах 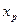многочлен 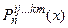принимает соответствующие значения:

( ;

( ;

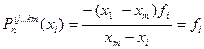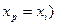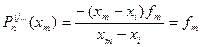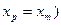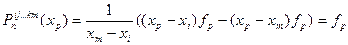
Вычисляя последовательно по формуле (4.43) значения… 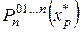, принимают их за последовательные приближения 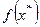. Процесс вычисления практически заканчивают, когда абсолютная величина разности двух последовательных приближений становится достаточно малой.