Интерполяционные многочлены Ньютона

Если точка интерполирования 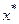находится в начале или в конце таблицы, то не всегда возможно выбрать достаточное количество узлов слева и справа от 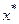для построения необходимых конечных разностей. В этом случае используются специальные формы интерполяционного многочлена.

Пусть точка 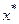расположена в близи первого узла сетки 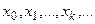. рассмотрим переменную t, определяемую соотношением (4.21), и построим интерполяционный многочлен.

Первый интерполяционный многочлен Ньютона обычно обозначается .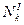

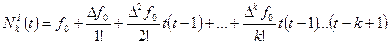. (4.30)

Остаточный член относительно переменной t можно представить в виде:

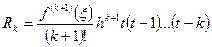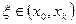; , (4.31)

а оценку погрешности приближенного значения 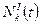(погрешности метода) – в виде:

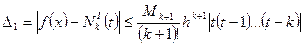, (4.32)

где .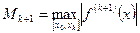

Пусть точка 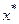расположена вблизи последнего узла сетки 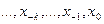. Для этой сетки, снова используя переменную t, определяемую соотношением (4.21), построим интерполяционный многочлен.

Второй интерполяционный многочлен Ньютона обычно обозначается .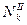

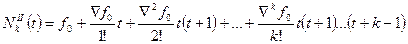. (4.33)

с остаточным членом

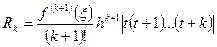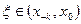, (4.34)

и оценкой погрешности приближенного значения

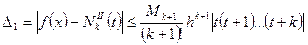, (4.35)

где .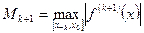

Формулы (4.30) и (4.33) часто называют соответственно интерполяционными формулами Ньютона для интерполирования вперед и назад.