Интерполяционные многочлены Стирлинга и Бесселя

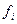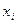Рассмотрим задачу построения интерполяционного многочлена для функции f, заданной своими значениями и равномерной сетки с шагом h.

Пусть точка х* расположена вблизи некоторого узла, который обозначим . Требуется построить интерполяционный многочлен четной степени. В качестве узлов интерполирования следует выбрать сетку, симметричную относительно узла :

Введем новую переменную t, с помощью которой начало отсчета переводится в точку :

; (4.21)

при этом .

Используя средние арифметические соседних конечных разностей одного и того же порядка 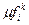, можно получить интерполяционный многочлен Стирлинга, обычно обозначаемый :

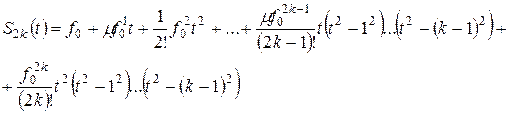(4.22)

Так как многочлен Стирлинга является лишь новой формой интерполяционного многочлена Лагранжа, построенного по узлам , то его остаточный член относительно переменной t можно представить в виде

; , (4.23)

а оценку погрешности приближенного значения (погрешности метода) – в виде

, (4.24)

где .

Пусть теперь точка интерполирования 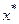лежит между узлами и 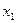в близи точки 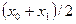. Требуется построить интерполяционный многочлен нечетной степени. Тогда сетка, минимизирующая погрешность, симметрична относительно точки 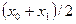, т.е. относительно точки .

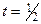На сетке 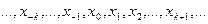можно получить интерполяционный многочлен Бесселя, обычно обозначаемый :

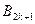(4.25)

Так как многочлен Бесселя является еще одним представлением интерполяционного многочлена Лагранжа, построенный по узлам 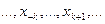, то его остаточный член относительно переменной t можно записать в виде:

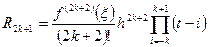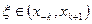, (4.26)

а оценку погрешности приближенного значения (погрешности метода) – в виде:

, (4.27)

где .

Итак, рассмотрено два интерполяционных многочлена: многочлен Стирлинга, который используется при построении многочлена четной степени и строится по нечетному числу узлов, и многочлен Бесселя, который используется при построении многочлена нечетной степени и строится по четному числу узлов.

Если же степень многочлена фиксирована не жестко, т.е. может быть как четной, так и нечетно, то целесообразно использовать многочлен Стирлинга в случае, когда

, (4.28)

т.е. когда точка интерполирования 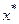расположена ближе к узлу 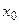, чем к середине между узлами. Многочлен Бесселя следует использовать в случае, когда

, (4.29)

т.е. когда точка интерполирования 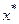расположена ближе к середине между узлами и . Одно из условий (4.28) или (4.29) всегда может быть обеспечено выбором соответствующего узла в качестве .