Интерполяционные формулы Ньютона.
Пусть интерполируемая функция задана значениями  на системе равноотстоящих узлов, таких что
на системе равноотстоящих узлов, таких что 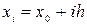 , где
, где 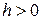 шаг сетки (таблицы) интерполяции.
шаг сетки (таблицы) интерполяции.
Определим конечные разности 1-го порядка:
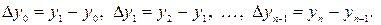
Число конечных разностей 1-го порядка табличной функции заданной 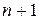 узлом равна
узлом равна 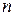 .
.
Определим конечные разности 2-го порядка:
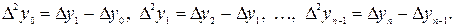
Для конечных разностей 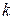 -того порядка:
-того порядка:
 , где
, где 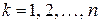 и
и  .
.
По определению 1-ая производная функции 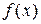 в точке
в точке 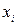 :
:
lim  lim
lim 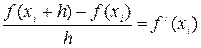 .
.
Следовательно, можно говорить о том, что отношение конечных разностей 1-го порядка к шагу интерполяционной таблицы является численным приближением первой производной интерполируемой функции в узлах интерполяции, т.е.:
 .
.
Рассмотрим связь конечных разностей 2-го порядка со второй производной интерполируемой функции:
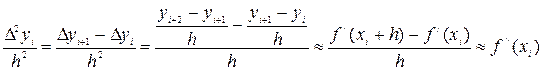
В общем случае можно говорить о связи между конечными разностями и производными интерполируемой функции 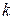 -того порядка:
-того порядка:
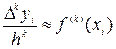 .
.
Интерполяционный полином 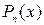 будем искать в виде:
будем искать в виде:
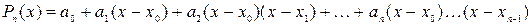 .
.
Необходимо определить 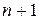 коэффициент
коэффициент 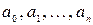 .
.
Из 1-го условия интерполяции получаем:

 .
.
То есть 1-ый коэффициент 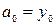 .
.
Из 2-го условия интерполяции получаем:

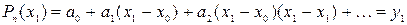
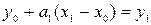 .
.
Таким образом, для второго коэффициента 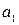 имеем:
имеем:
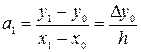 .
.
Рассмотрим 3-е условие интерполяции:
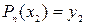
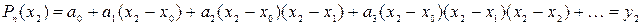
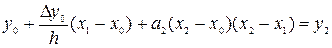
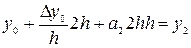
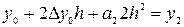 .
.
Для коэффициента 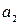 можно записать:
можно записать:
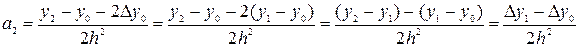



Введем следующее обозначение:
 .
.
Тогда можно записать:

Таким образом, 1-ая интерполяционная формула Ньютона (формула для интерполирования слева):
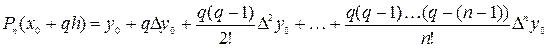
Разделенные разности 1-го порядка.
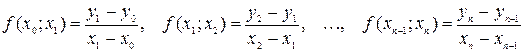
Разделенные разности 2-го порядка.
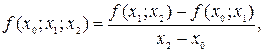
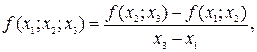
…
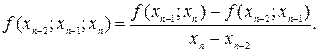
Разделенные разности k-го порядка:
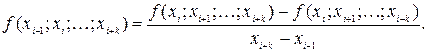
Формула Ньютона для интерполирования с непостоянным шагом:
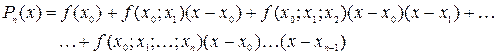
Дата добавления: 2015-11-20; просмотров: 1076;
