Формула прямоугольника.
При замене интеграла интегральными суммами возникает вопрос в каком месте выбрать узел, чтобы интеграл вычислялся как можно точнее. Оказывается, что если точка выбирается в середине интервала интегрирования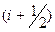 
, то в этом случае погрешность получается минимальной. Оценим эту погрешность.
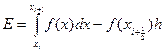
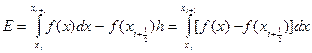
Разложим функцию f(x) относительно точки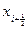 
в ряд Тейлора, тогда получим следующую зависимость:
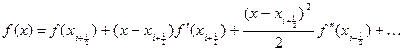
Ограничимся тремя членами, в данном случае этого достаточно.
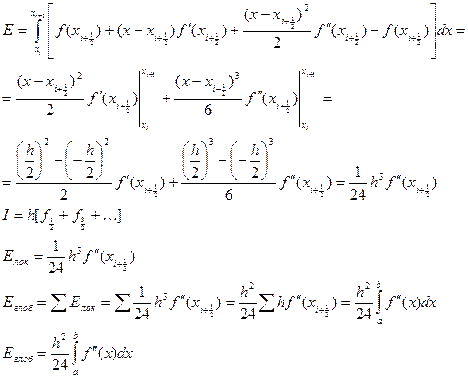
Вычисленная локальная погрешность для метода прямоугольника будет равна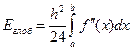 
, соответственно глобальная погрешность составит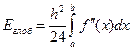
Формула трапеций.
 |
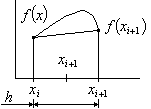Проведем прямую через две заданных точки вначале и конце интервала. Такое решение является не оптимальным, оно приводит к увеличению погрешности даже по сравнению с методом прямоугольника, в котором для вычисления интеграла используется только одна точка.
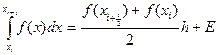
Задача состоит в том, чтобы вычислить погрешность такой замены.
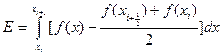
Для вычисления этих значений используется разложение в ряд Тейлора относительно точек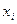 
и 
.
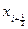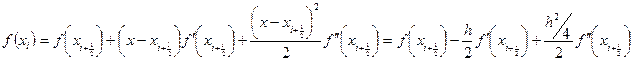
Аналогично разложим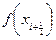 
и получим:
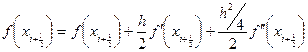
Сложим обе функции
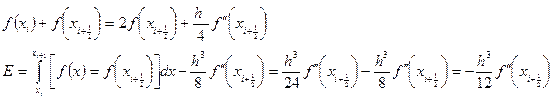
Как видим, погрешность для метода трапеций получилась в два раза больше, чем для метода прямоугольников.
Глобальная погрешность для метода трапеций может быть вычислена следующим образом:
Дата добавления: 2015-11-20; просмотров: 740;