Лекция №15. Итерационные методы решения систем нелинейных уравнений.

Продолжительность: 2 часа (90 мин.)

Лекция №16. Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера.

Продолжительность: 2 часа (90 мин.)

Дифференциальным уравнением n-го порядка называется уравнение вида:

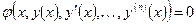, где

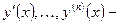производные 1,…,n-го порядков.

Условия однозначности выделяют из некоего множества решений одно единственное. Условия могут быть заданы различными способами. И в зависимости от этих способов мы можем выделить следующие классы задач:

1. Задачи с начальными условиями (задача Коши). Для этого типа задач значения функции 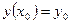, 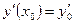и т.д., задаются в одной точке.

2. Краевые задачи – не все условия задаются в одной точке. Количество условий должно совпадать с порядком дифференциального уравнения.

Метод Эйлера.

Решение:

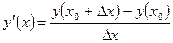- левая производная.

Мы берем эту аппроксимацию и подставляем ее в дифференциальное уравнение.

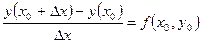
Отсюда мы можем построить решение на шаге .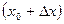

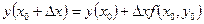
Если это отобразить в некой системе координат, то получим:

Теперь нужно провести оценку точности решения. Воспользуемся способом, который состоит в следующем: 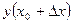– точное решение дифференциального уравнения, разлагаем в ряд Тейлора в близи точки .

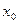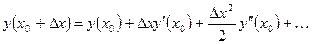
Мы можем получить любое приближение если нам известны значения производных.

Точное решение нашего уравнения и приближенное, решенное по методу Эйлера, отличаются на .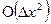

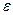- погрешность для одного интервала,

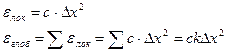
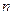- число интервалов, на которых ищется данное решение,

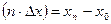, т.е.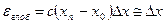

Это достаточно большая погрешность.