Метод половинного деления.

Этот метод не обладает высокой скоростью сходимости, но весьма надежен.

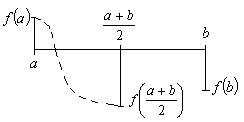
Если функция имеет такой вид, то берем за крайнюю точку 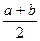и продолжаем делить следующий интервал до того пока не будет выполнено условие останова:

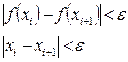Для непрерывной функции эти условия эквивалентны.

Алгоритм половинного деления:

1. Вычислить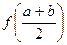

2. Если 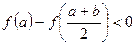, то ,

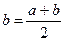Иначе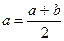

3. Если 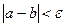, то 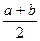- корень нашего уравнения,

Иначе перейти к 1.

Метод простой итерации.

Исходное уравнение нужно записать в виде 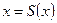. Это можно сделать следующим образом:

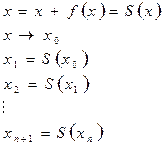
Этот ряд нужно продолжить пока .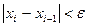

Метод сходится если выполнено условие .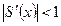

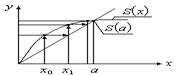
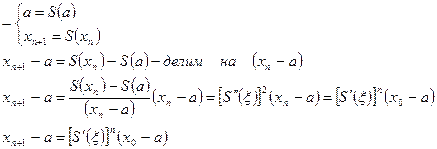
Корень будет сходиться если .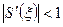

Метод Ньютона.

1. В нулевой точке нужно определить значение касательной .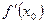

2. Проводим касательную до пересечения с осью абсцисс, получаем второе приближение и т.д.

Эта схема является очень эффективной, скорость сходимости квадратична.

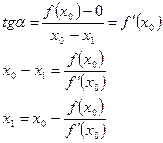
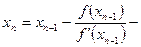Формула Ньютона, которая и дает возможность построить алгоритм.

Недостатки:

- нужно вычислять значение производной (операция вычисления производной является некорректной).

- для метода Ньютона необходимо очень аккуратно выбирать начальную точку приближения.

Метод секущих.

Основан на замене производной 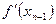конечно-разностной аппроксимацией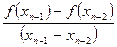

Если подставить это значение в формулу Ньютона, то получится метод секущих.

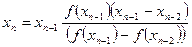
Недостатки:

- необходимо увеличить количество переменных для хранения величин 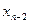, т.е. полученных на предыдущем шаге.

- скорость меньше, чем у метода Ньютона.