Постановка задачи интерполяции.

Задача интерполирования состоит в том, чтобы по значениям функции f(x) в нескольких точ­ках отрезка восстановить ее значения в остальных точках этого отрезка. Разумеется, такая задача допускает сколь угодно много решений. Задача интерполирования возникает, например, в том случае, когда известны результаты измерения y_h=f(x_k) некоторой физической величины f(x) в точках х_к, к=0, 1, ..., к, и требуется определить ее значения в других точках. Интерполирование используется также при сгущении таблиц, когда вычисление зна­чений /(х) трудоемко. Иногда возникает необходимость приближенной замены или аппроксимации данной функции другими функциями, которые легче вычислить. Результаты и методы теории интерполирования и приближения функций нашли широкое применение в численном анализе, например при выводе формул численного дифференцирования и интегрирования, при построении сеточных аналогов задач математической физики.

Метод Лагранжа.

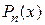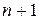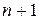Найти полином означает определить значения его коэффициента . Для этого используя условие интерполяции можно сформировать систему линейных алгебраических уравнений (СЛАУ).

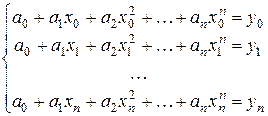
Определитель этой СЛАУ называется определителем Вандермонда. Определитель Вандермонда не равен нулю при для 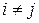, то есть в том случае, когда в интерполяционной таблице нет совпадающих узлов. Таким образом, можно утверждать, что СЛАУ имеет решение и это решение единственно. Решив СЛАУ и определив неизвестные коэффициенты можно построить интерполяционный полином .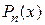

Полином, удовлетворяющий условиям интерполяции, при интерполяции методом Лагранжа строится в виде линейной комбинации многочленов n-ой степени:

.

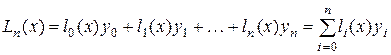Многочлены 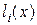называется базисными многочленами. Для того, чтобы многочлен Лагранжа удовлетворял условиям интерполяции необходимо, чтобы для его базисных многочленов 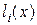выполнялись следующие условия:

для .

Если эти условия выполняются, то для любого 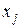имеем:

.

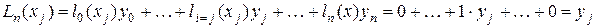Таким образом, выполнение заданных условий для базисных многочленов означает, что выполняются и условия интерполяции.

Определим вид базисных многочленов исходя из наложенных на них ограничений.

1-е условие: 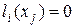при .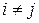

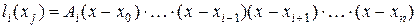
2-е условие: .

, т.е.

.

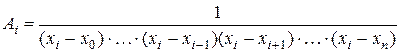Окончательно для базисного многочлена 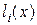можно записать:

.

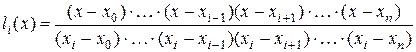Тогда, подставляя полученное выражение для базисных многочленов в исходный полином, получаем окончательный вид многочлена Лагранжа:

.

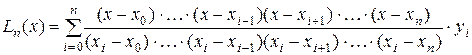Частная форма многочлена Лагранжа при 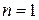называется формулой линейной интерполяции:

.

Многочлен Лагранжа взятый при 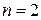называется формулой квадратичной интерполяции:

.