Примеры реализации.
Задача.
Решить СЛАУ 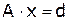 методом прогонки:
методом прогонки:
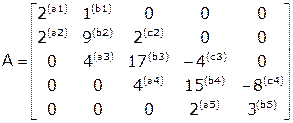 ,
, 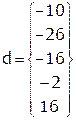 .
.
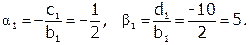
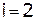
|
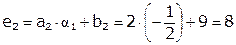 .
.
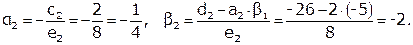
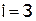
|
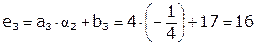 .
.
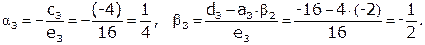

|
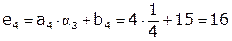 .
.
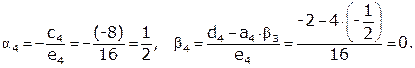
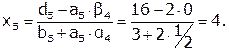

|
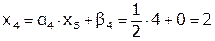
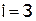
|
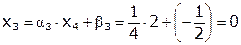
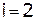
|
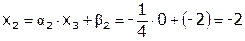
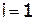
|
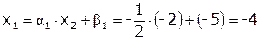
Решение 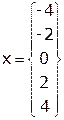
Лекция №5. Итерационные методы решения СЛАУ. Метод Якоби. Метод Зейделя. Метод верхней релаксации.
Продолжительность: 2 часа (90 мин.)
Метод Якоби.
Исходная система  может быть преобразована к эквивалентной системе вида:
может быть преобразована к эквивалентной системе вида:
 , где
, где
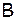 - некоторая новая матрица;
- некоторая новая матрица;
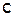 - некоторый новый вектор.
- некоторый новый вектор.
Метод простой итерации (МПИ) предполагает нахождение решения системы  путем вычисления последовательных приближений с помощью рекуррентного равенства:
путем вычисления последовательных приближений с помощью рекуррентного равенства:
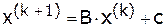 , где
, где
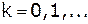 - номер итерации, а
- номер итерации, а 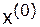 - некоторое начальное приближение. Матрица
- некоторое начальное приближение. Матрица 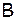 называется матрицей итерирования или перехода.
называется матрицей итерирования или перехода.
Необходимым и достаточным условием сходимости метода простой итерации при любом начальном приближении 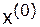 к решению системы
к решению системы  является требование, чтобы все собственные числа матрицы перехода
является требование, чтобы все собственные числа матрицы перехода 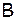 были по модулю меньше 1.
были по модулю меньше 1.
Устойчивый способ разложения 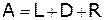 .
.
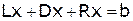

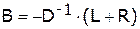 ,
, 
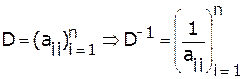
В развернутом виде полученное матричное уравнение можно записать следующим образом:
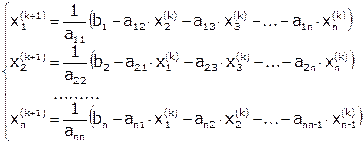
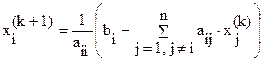
Достаточный признак сходимости метода Якоби.
Метод Якоби сходится в случае диагонального преобладания в матрице коэффициентов СЛАУ:
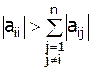 , где
, где  .
.
Метод Зейделя.
Метод Зейделя можно рассматривать как модификацию метода Якоби. Основная идея метода состоит в том, чтобы использовать вычисленные компоненты вектора 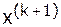 уже на текущей итерации, а не на следующей.
уже на текущей итерации, а не на следующей.
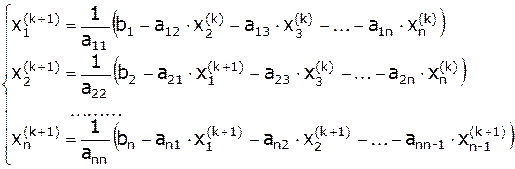
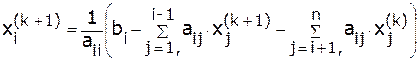

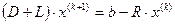
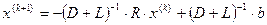 , т.е.:
, т.е.:
 ,
,  .
.
Система  называется нормальной, если матрица
называется нормальной, если матрица  является симметричной и положительно определена, т.е.
является симметричной и положительно определена, т.е. 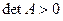 .
.
Достаточный признак сходимости метода Зейделя: если исходная система  нормальная, то метод Зейделя сходится.
нормальная, то метод Зейделя сходится.
Если исходная система не является нормальной, то ее можно привести к нормальному виду с помощью симметризации Гаусса – путем домножения левой и правой части матричного уравнения на транспонированную матрицу коэффициентов  :
:
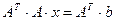 .
.
Дата добавления: 2015-11-20; просмотров: 1143;
