Лекция №3. Прямые методы решения систем линейных алгебраических уравнений. Метод Жордана-Гаусса. Обращение матрицы.
Продолжительность: 2 часа (90 мин.)
Метод Жордана-Гаусса.
Исходная система.
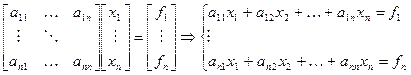
Для метода Жордана-Гаусса реализуются следующие этапы.
1. Нормализация строки. (также как и в методе Гаусса).
1-ю строку делим на 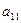 , затем умножаем на
, затем умножаем на 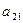 и из 2-ой строки вычитаем 1-ю. Такую операцию проделываем с остальными строками.
и из 2-ой строки вычитаем 1-ю. Такую операцию проделываем с остальными строками.
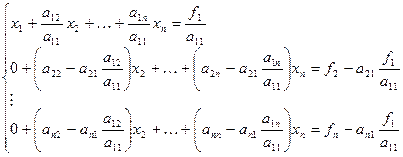
2. Преобразование матрицы к диагональной.
Указанным выше способом преобразовываем исходную матрицу к диагональной.
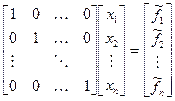
Обращение матрицы.
Обращение матрицы.
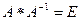 , где
, где 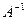 - обратная матрица и Е – единичная матрица
- обратная матрица и Е – единичная матрица
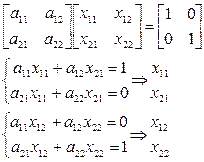
Нахождение обратной матрицы при помощи метода Жордана-Гаусса.
Исходная матрица
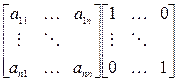
Преобразуем исходную матрицу к единичной, используя метод Жордана и при этом совершаем преобразования и над единичной матрицей.
Обратная матрица
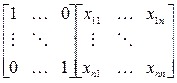
Лекция №4. Прямые методы решения систем линейных алгебраических уравнений. Метод прогонки. Примеры реализации.
Продолжительность: 2 часа (90 мин.)
Метод прогонки.
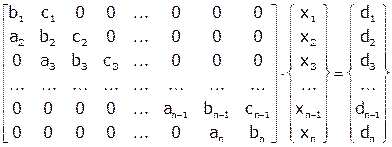
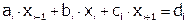 , где
, где 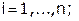
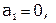
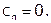
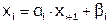 , где
, где 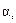 и
и 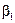 - прогоночные коэффициенты.
- прогоночные коэффициенты.
Первое уравнение.
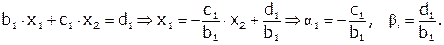
Второе уравнение.
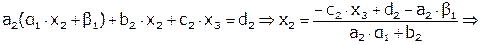
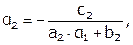
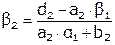 .
.
Обозначим 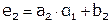 , тогда
, тогда 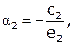
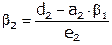 .
.
Третье уравнение.
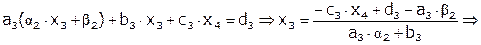
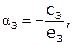
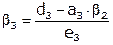 , где
, где 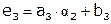 .
.
i-тое уравнение.
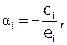
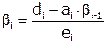 , где
, где 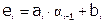 .
.
Вычисление 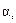 и
и 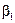 для
для 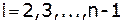 – прямая прогонка.
– прямая прогонка.
Из уравнений n и n-1 имеем:
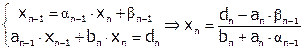 .
.
Обратная прогонка состоит в последовательном вычислении неизвестных с помощью прогоночных коэффициентов:
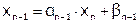 ,
,
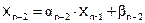 ,
,
… ,
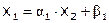 .
.
Алгоритм решения СЛАУ методом прогонки:
1) 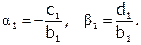
2) Для 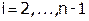 :
:
3) 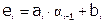 .
.
4) 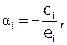
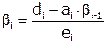 .
.
5) 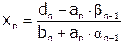 .
.
6) Для 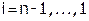 (шаг -1):
(шаг -1):
7) 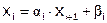 .
.
Метод прогонки корректен при 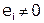 и устойчив при
и устойчив при 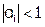 . Достаточное условие, обеспечивающее устойчивость метода:
. Достаточное условие, обеспечивающее устойчивость метода:
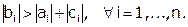
Дата добавления: 2015-11-20; просмотров: 1749;
