Классификация методов решения СЛАУ.

Задача решения СЛАУ формулируется как вопрос численного решения систем вида:

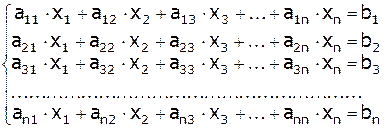(2.1)

Или, в векторно-матричной форме:

,

где – вектор правой части;

– вектор неизвестных;

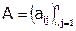– матрица коэффициентов системы.

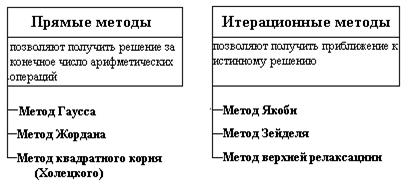
Все методы решения СЛАУ можно разделить на два класса: прямые и итерационные методы.

Прямые методы– используют конечные соотношения (формулы), которые приводят к решению за известное конечное число арифметических операций. Если арифметические операции реализуются точно, то и получаемое решение СЛАУ также будет точным.

Итерационные методы – это методы последовательных приближений к решению, получаемых путем повторения циклов вычислений, называемых итерациями. Результатом проведения итерации является получение очередного приближения к решению. Итерации проводятся до получения решения с заданной точностью. Объем вычислений при использовании методов данного класса заранее определить трудно.

В качестве примера сопоставим трудозатраты для решения СЛАУ методом Крамера и методом Гаусса.

Пример: В методе Крамера количество операции (умножения) для решения СЛАУ размером n на n равно n!.

В методе Гаусса количество операций (умножения) для решения СЛАУ размером n на n равно .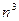

Проведем оценку экономичности методов для разных размерностей СЛАУ:

для n=2

· метод Крамера - n!=2

· метод Гаусса - 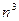=8

для n=10

· метод Крамера - n!=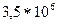

· метод Гаусса -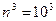

Из приведенных оценок видно, что метод Крамера лучше всего подходит для малых размерностей СЛАУ, начиная с размерности n=6 более эффективным становится метод Гаусса.

Метод Гаусса

Наиболее распространенным способом решения систем вида (2.1) является метод Гаусса. Суть данного метода состоит в последовательном исключении неизвестных.

Прямой ход метода Гаусса предполагает поэтапное приведение исходной системы СЛАУ к эквивалентной треугольной системе вида:

(2.2)

Затем, в ходе обратного хода метода Гаусса, из n-ого уравнения преобразованной системы (2.2), которое содержит только один элемент вектора неизвестных, находится значение последнего коэффициента вектора неизвестных - 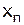. Подставляя полученное значение в (n-1)-ое уравнение, которое содержит два элемента вектора неизвестных, находим значение и т.д., пока из 1-го уравнения не находим значение , полностью определив вектор неизвестных.

На 1-ом этапе прямого хода метода Гаусса исходная система СЛАУ приводится к виду:

(2.3)

Коэффициенты системы (2.3) вычисляются как результат эквивалентных преобразований исходной системы (2.1).

Выпишем коэффициенты 1-ой и 2-ой строки исходной системы:

,	,	,	…,	,
,	,	,	…,	,

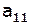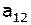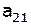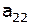Разделим 1-ую строку на ее диагональный коэффициент:

,

,

,

…,

,

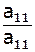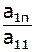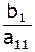
Затем умножим 1-ую строку на первый коэффициент второй строки:

,

,

,

…,

,

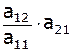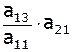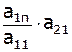Далее вычитаем получившиеся коэффициенты 1-ой строки из коэффициентов 2-ой строки:

, , , …, , .

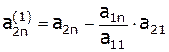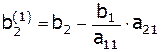Таким образом, формулы для преобразования элементов второй строки системы уравнений:

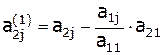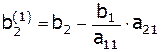, , где .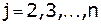

Аналогичным образом выводим формулы для третьей и последующих строк:

, ,

…,

, ,

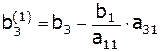где .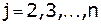

Окончательные формулы для 1-го этапа прямого хода метода Гаусса:

, ,

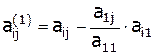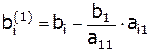где .

Второй этап прямого хода метода Гаусса.

Формулы для 2-го этапа прямого хода метода Гаусса:

, ,

где .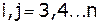

Этап (n-1) прямого хода метода Гаусса.

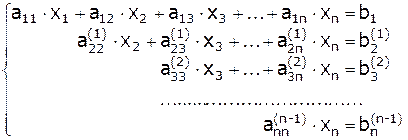
Формулы для (n-1)-го этапа прямого хода метода Гаусса:

, ,

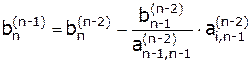здесь .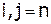

Таким образом, окончательная формула расчета коэффициентов СЛАУ для прямого хода метода Гаусса:

, ,

где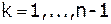

.

Обратный ход:

;

;

……………

;

.

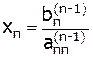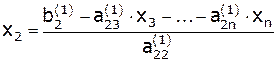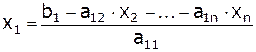Формула для обратного хода метода Гаусса:

,

где .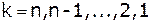

Алгоритм решения СЛАУ методом Гаусса:

1. Для :

2. Для :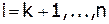

3. ;

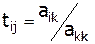4. ;

5. Для :

6. ;

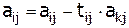7. ;

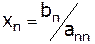8. Для

9. .