Лекция №11. Формула Симпсона. Квадратурная формула Гаусса.
Продолжительность: 2 часа (90 мин.)
Метод Симпсона.
 |
 |
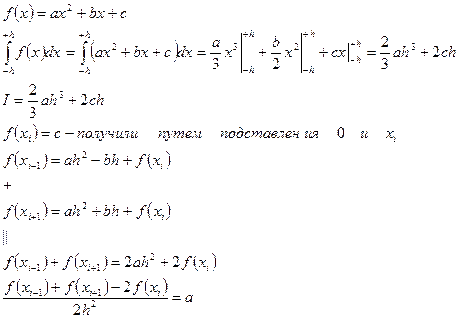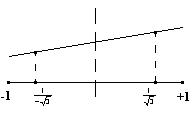
Заменим исходную интегрируемую функцию параболой, проходящую через три выбранные точки, и вычислим интеграл под выбранной параболой. Для упрощения расчетов сместим систему координат так, как представлено на рисунке. Отметим, что вычисленное значение интеграла при этом не изменится. При этом имеем:
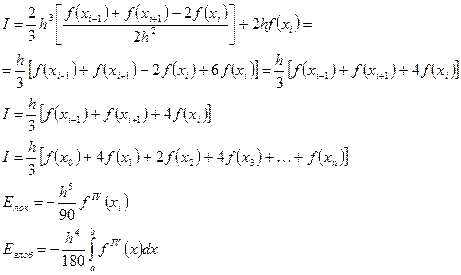
11.2.Квадратурная формула Гаусса.
Рассмотренные ранее методы предполагали, что узлы в выбранных методах заданы. Но можно подобрать узлы так, чтобы обеспечить максимальную точность вычисления интеграла, или получить точное значение для алгебраического многочлена возможно большей степени.
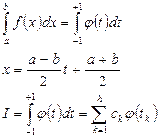
Количество коэффициентов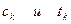 
будет равно 2n.
Поставим задачу точного интегрирования некоторого полинома степени n, для полинома степени 2n-1 будет 2n известных коэффициентов. Задача получается такой, что для степени 2n-1 можно подобрать столько неизвестных, чтобы получился интеграл с наибольшей точностью.
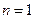– полином первой степени.
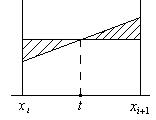
Метод прямоугольников, метод наивысшей точности для полинома первой степени.
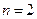–полином третьей степени.
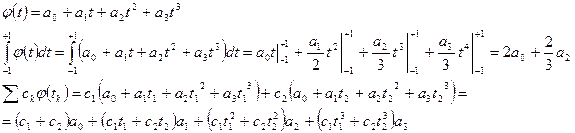
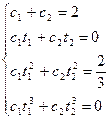- система из 4-х неизвестных, кот. может быть решена, и имеет такие решения:
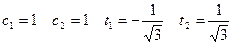
Дата добавления: 2015-11-20; просмотров: 1860;