Другий закон Ньютона для обертового руху
Візьмемо похідну від 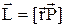 по часу
по часу
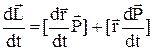 . (1)
. (1)
Перший доданок у правій частині (1) дорівнює 0, тому що маємо векторний добуток паралельних векторів - швидкості тіла та його імпульсу. У другому доданкові за другим законом Ньютона 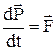 і остаточно маємо рівняння руху у вигляді
і остаточно маємо рівняння руху у вигляді
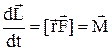 . (2)
. (2)
Підставивши в (2) вираз для моменту імпульсу 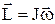 одержимо
одержимо
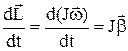 . (3)
. (3)
Прирівнюючи праві частини (2) та (3), одержимо
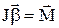 . (4)
. (4)
Вирази (3) та (4) представляють собою рівняння другого закону Ньютона для обертового руху. З (4) можна зробити висновок про фізичний зміст моменту інерції J, а саме, момент інерціїє мірою інертності тіла відносно моменту сили, що діє на нього. При дії на тіло моменту сили 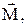 воно буде обертатися з більшим кутовим прискоренням
воно буде обертатися з більшим кутовим прискоренням 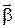 при меншому моментові інерції J.
при меншому моментові інерції J.
2.12.4. Кінетична енергіятіла, що обертається
Нехай тверде тіло з густиною r обертається відносно деякої осі з кутовою швидкістю w. Знайдемо кінетичну енергію обертового руху цього тіла. Розіб'ємо тіло на точкові частинки з масою dm=rdV, що мають радіус обертання r, об'єм dV і лінійну швидкість wr. Такі частинки мають кінетичну енергію
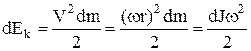 , (1)
, (1)
а енергія тіла
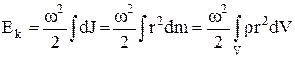 . (2)
. (2)
У виразі (2) інтеграл по об'єму тіла 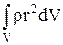 дорівнює моментові інерції тіла J, а тому кінетична енергія тіла запишеться у такому виді
дорівнює моментові інерції тіла J, а тому кінетична енергія тіла запишеться у такому виді
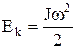 . (2)
. (2)
2.12.5. Момент інерції деяких тіл
Момент інерції макроскопічного тіла можна знайти розбиттям тіла на нескінченно малі маси 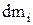 і розглянути їх як точкові. При цьому момент інерції тіла дорівнює сумі моментів інерції його складових
і розглянути їх як точкові. При цьому момент інерції тіла дорівнює сумі моментів інерції його складових
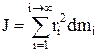
або
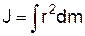 .
.
Застосовуючи цей метод, розглянемо момент інерції деяких тіл.
а). Момент інерціїJ тонкого обруча маси m і радіусом R відносно осі, що проходить через центр, перпендикулярно його площині, дорівнює J=mR2. Дійсно, якщо розбити обруч на нескінченно малі дуги з масами dm, які мають радіус обертання 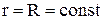 , то
, то 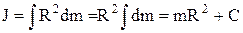 . При R=0, J=0 і тоді С=0, а
. При R=0, J=0 і тоді С=0, а 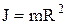 .
.
б). Момент інерції J циліндрамаси m із радіусом основи R відносно його осі дорівнює J=mR2/2.
Дійсно, розіб'ємо циліндр на концентричні обручі радіуса х із нескінченно малою товщиною dx, момент інерції яких буде дорівнювати dJ=x2dm, де dm=2px×dx×h×r ¾ елемент маси обруча, h ¾ висота циліндра, r ¾ його густина. Тепер момент інерції циліндра можна обчислити так:
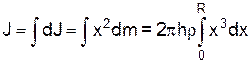
J= 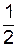 phrR4=
phrR4= 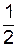 (pR2hr)R2=
(pR2hr)R2=  mR2.
mR2.
Момент інерції J дискамаси m із радіусом основи R відносно осі, що проходить через центр мас, перпендикулярно його площині, дорівнює J=  mR2. Ми зважили, що диск за формою є циліндром.
mR2. Ми зважили, що диск за формою є циліндром.
в). Момент інерції циліндричного кільцямаси m із внутрішнім радіусом R1 і зовнішнім R2 відносно його осі дорівнює:
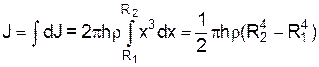 ,
,
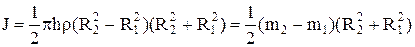
і остаточно
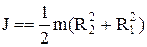 ,
,
де 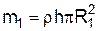 ¾ маса циліндра з радіусом основи R1,
¾ маса циліндра з радіусом основи R1, 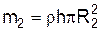 ¾ маса циліндра з радіусом основи R2, а m=m2-m1-маса кільця.
¾ маса циліндра з радіусом основи R2, а m=m2-m1-маса кільця.
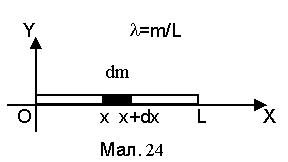 г). Момент інерції J прямолінійного стержнямаси m і довжини L відносно осі, що проходить через початок, перпендикулярно йому (див.Мал.24). Момент інерції стержня запишемо у вигляді
г). Момент інерції J прямолінійного стержнямаси m і довжини L відносно осі, що проходить через початок, перпендикулярно йому (див.Мал.24). Момент інерції стержня запишемо у вигляді 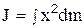 , де dm=ldx, a l¾лінійна густина стержня. Тепер розрахуємо інтеграл
, де dm=ldx, a l¾лінійна густина стержня. Тепер розрахуємо інтеграл
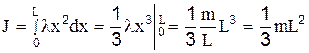 .
.
Якщо вісь обертання проходить через середину стержня, для визначення моменту інерції досить змінити границі з Î[0,L] на xÎ[-L/2,L/2]. Тепер
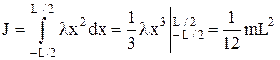 .
.
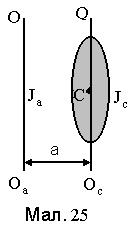 Момент інерції J кулімаси m із радіусом R відносно осі, що проходить через центр кулі, дорівнює
Момент інерції J кулімаси m із радіусом R відносно осі, що проходить через центр кулі, дорівнює 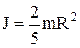 .
.
Дата добавления: 2015-09-18; просмотров: 4251;
