Сили тертя та сили опору.
Сила тертя¾ це сила, що виникає при взаємодії тіл дотичними поверхнями. Якщо при дії іншого тіла, дане тіло буде нерухомим, то така сила тертя є силою тертя спокою, у противному разі ¾ сила тертя ковзання.
Сила 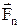 , яка діє на поверхню в перпендикулярному до неї напрямкові, називається силою нормального тиску.
, яка діє на поверхню в перпендикулярному до неї напрямкові, називається силою нормального тиску.
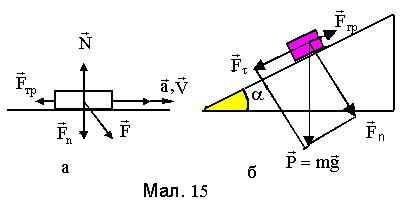 |
Нехай на тіло, що рухається на деякій поверхні (див.Мал. 15 а) із швидкістю
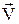 , діє сила
, діє сила 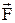 . Під дією цієї сили виникає сила тертя ковзання
. Під дією цієї сили виникає сила тертя ковзання 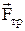 , направлена протилежно напрямкові швидкості тіла
, направлена протилежно напрямкові швидкості тіла 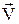 . За величиною сила
. За величиною сила 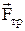 пропорційна величині сили
пропорційна величині сили 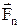 нормального тиску
нормального тиску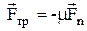 , де m ¾ коефіцієнт тертя. Сила тертя спокою за величиною дорівнює тангенціальній складовій зовнішньої сили і має протилежний їй напрямок. Сила тертя не залежить від величини дотичних поверхонь і швидкості тіла.
, де m ¾ коефіцієнт тертя. Сила тертя спокою за величиною дорівнює тангенціальній складовій зовнішньої сили і має протилежний їй напрямок. Сила тертя не залежить від величини дотичних поверхонь і швидкості тіла.
Розглянемо стан тіла на похилій площині з кутом нахилу a, який визначається величиною коефіцієнта тертя та кутом нахилу площини. Тіло буде знаходитися в стані спокою, коли величини тангенціальної сили та сили тертя мають співвідношення Fтр³Ft. З простих міркувань маємо (див.Мал. 15 б) Ft=mgsina та Fтр=mFn=mmgcosa. При tga > m, тіло буде ковзати вниз по похилій площині з прискоренням, при tga=m - здійснювати рівномірний прямолінійний рух або знаходитися в стані спокою, при tga<m тіло буде покоїться на площині.
Силою опору 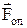 називається сила взаємодії між тілом та середовищем, у якому воно рухається. Таким середовищем може бути рідина або газ. Сила опору в газі має напрямок протилежний напрямкові швидкості тіла
називається сила взаємодії між тілом та середовищем, у якому воно рухається. Таким середовищем може бути рідина або газ. Сила опору в газі має напрямок протилежний напрямкові швидкості тіла 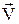 , пропорційна швидкості
, пропорційна швидкості 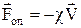 , а при великих швидкостях ¾ квадрату швидкості Fоп=-c'V2, де c та c¢ ¾ коефіцієнти опору. Сила опору в рідині при невеликих швидкостях тіла також пропорційна швидкості. Наприклад, у випадку кульки радіуса r, що рухається в рідині із швидкістю V, сила опору визначається за формулою Стокса
, а при великих швидкостях ¾ квадрату швидкості Fоп=-c'V2, де c та c¢ ¾ коефіцієнти опору. Сила опору в рідині при невеликих швидкостях тіла також пропорційна швидкості. Наприклад, у випадку кульки радіуса r, що рухається в рідині із швидкістю V, сила опору визначається за формулою Стокса
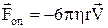 .
.
де h ¾ коефіцієнт опору (динамічний коефіцієнт в'язкості).
2.6.3. Сили інерції
Нехай на матеріальну точку А з масою m діє сила 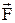 . Рівняння її руху в інерціальній системі запишеть у вигляді
. Рівняння її руху в інерціальній системі запишеть у вигляді
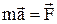 . (1)
. (1)
Для одержання рівняння руху тіла в неінерційній системі К', скористуємось рівнянням (14) п.1.6.2. Прискорення в системі К' має вид
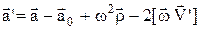 .
.
Домноживши його на масу матеріальної точки одержимо
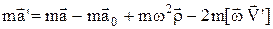 (2)
(2)
Вираз (2) можна представити у вигляді
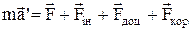 . (3)
. (3)
де
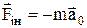 (4)
(4)
- поступальна сила інерції,
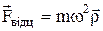 (5)
(5)
-відцентрова сила інерції,
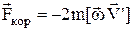 (6)
(6)
коріолісова сила інерції.
Сила (4) зявляється лише тоді, коли система К¢ здійснює прискорений поступальний рух. Якщо система К¢ обертається з деякою кутовою швидкістю, то на тіло, нерухоме в системі К¢, діє відцентрова сила інерції (5) і, коли воно починаає рухатись, виникає коріолісова сила інерції (6).
Перелічені сили інерції зумовлені лише властивостями неінерційної системи К¢ і відсутні в інерційних системах відліку.
2.7. Робота сили та її обчислення. Потужність. Енергія
2.7.1. Робота й потужність.
Роботає характеристикою дії сили. У процесі роботи відбувається перетворення енергії одного тіла чи системи тіл в енергію другого тіла чи системи тіл, при цьому витрачувана й створювана енергії можуть різниться за своїм видом. Елементарна робота дорівнює скалярному добуткові сили на переміщення
dA= 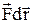 , dA=Fdr×cosa=Ftdr, (1)
, dA=Fdr×cosa=Ftdr, (1)
де 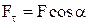 -тангенціальна складова сили, a ¾ кут між
-тангенціальна складова сили, a ¾ кут між 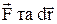 . Робота є безконтактним способом передачі енергії від одного тіла до іншого, а її величина є мірою переданої енергії.
. Робота є безконтактним способом передачі енергії від одного тіла до іншого, а її величина є мірою переданої енергії.
Потужність силиабо системи сил чисельно дорівнює роботі, яку вони виконують за одиницю часу
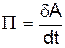 . (2)
. (2)
Для механічного руху, що відбувається під дією сталої у часі сили, можна записати
dА= 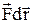 i
i 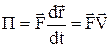 . (3)
. (3)
Потужність є динамічною характеристикою джерел енергії, а ефективністю застосування такого джерела є коефіціент корисної дії (ККД)
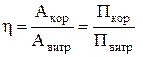 , (4)
, (4)
де 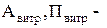 витрачені робота і потужність,
витрачені робота і потужність, 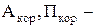 корисні робота і потужність. У реальних процесах
корисні робота і потужність. У реальних процесах 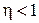 .
.
Якщо сила задана у явному вигляді як функція радіус-вектора положення тіла, то роботу можна знайти прямим інтегруванням
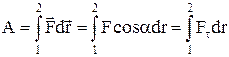 . (5)
. (5)
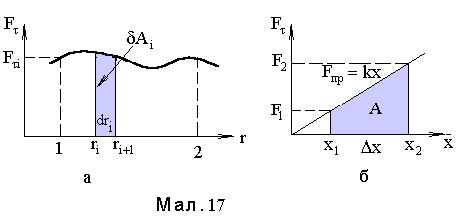
При графічному представленні сили як функції радіус-вектора положення тіла (див.Мал.17 а), то роботу можна знайти шляхом обчислення площі криволінійної трапеції, як суми елементарних робіт dАі. У випадку невеликого розтягування пружини з коефіцієнтом жорсткості k, указана трапеція буде звичайною з основами 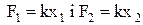 і висотою
і висотою 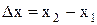 (див.Мал.17б). Таким чином площа трапеції, а з нею і робота проти пружної сили дорівнює
(див.Мал.17б). Таким чином площа трапеції, а з нею і робота проти пружної сили дорівнює
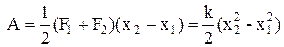 . (6)
. (6)
 |
Такий саме результат можна одержати шляхом інтегрування за формулою (5), де
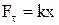
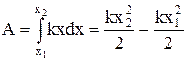 . (7)
. (7)
2.7.2. Кінетична та потенціальна енергія тіла.
Енергія¾ це міра спроможності тіла або поля виконати певну роботу.
Кінетична енергія є енергія тіла, що рухається і вона визначається рівністю
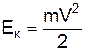 . (1)
. (1)
Потенціальнаенергія тіла визначається силою взаємодії між тілами (див.п.2.6.1) і залежить від їх взаємного розташування.
Розглянемо потенціальну енергію 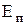 тіл для деяких взаємодій.
тіл для деяких взаємодій.
1. Електростатична взаємодія
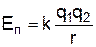 . (2)
. (2)
2. Гравітаційна взаємодія
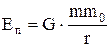 . (3)
. (3)
3. Взаємодія в полі земного тяжіння при поверхні Землі на висоті h
Eп=mgh. (4)
4. Енергія пружної взаємодії
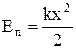 . (5)
. (5)
Дійсно, для електростатичної та гравітаційної взаємодій сила взаємодії обернено пропорційна квадратові відстані r між тілами (див.2.6.1.): 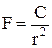 , а робота
, а робота
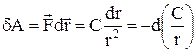 (6)
(6)
виконується за рахунок (убутку) потенціальної енергії, тобто
 , (7)
, (7)
і тоді
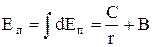 , (8)
, (8)
де В ¾ стала інтегрування. Для кулонівської взаємодії С=kqq0, а для гравітаційної С=Gmm0. При 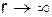 сили взаємодії зникають, і тому B=0, а енергія
сили взаємодії зникають, і тому B=0, а енергія 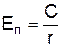 . Підставляючи у (8) відповідні значення величин С, одержимо наведені вище вирази для потенціальних енергій електричного та гравітаційного полів.
. Підставляючи у (8) відповідні значення величин С, одержимо наведені вище вирази для потенціальних енергій електричного та гравітаційного полів.
Для доведення виразу (4), підставимо у (3) r=Rз+h, де Rз - радіус Землі, h - висота тіла над Землею, причому Rз>>h, та введемо масу Землі m0=Mз
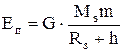 . (9)
. (9)
Проведемо в (9) ряд очевидних послідовних перетворень
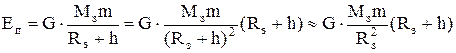 , (10)
, (10)
 У (10) величина
У (10) величина 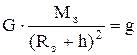 є прискоренням вільного падіння і тоді
є прискоренням вільного падіння і тоді
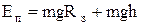 . (11)
. (11)
В (11) величина 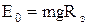 є потенціальної енергією взаємодії Землі й тіла, що знаходиться на її поверхні й є сталою величиною. Від Е0 власне й починається відлік потенціальної енергії тіла, при зміні його висоти над поверхнею Землі, тобто
є потенціальної енергією взаємодії Землі й тіла, що знаходиться на її поверхні й є сталою величиною. Від Е0 власне й починається відлік потенціальної енергії тіла, при зміні його висоти над поверхнею Землі, тобто
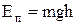 . (12)
. (12)
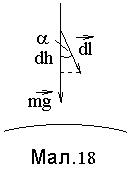
Вираз (12) можна одержати у такий спосіб. При поверхні Землі на тіло діє сила тяжіння 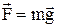 , яка переміщує його на
, яка переміщує його на 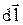 (див.Мал.18). При цьому нею буде виконана робота
(див.Мал.18). При цьому нею буде виконана робота 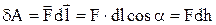 . Якщо тіло переміститься на висоту h, то при цьому буде виконана робота
. Якщо тіло переміститься на висоту h, то при цьому буде виконана робота 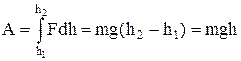 . Ця робота піде на створення потенціальної енергії
. Ця робота піде на створення потенціальної енергії 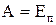 .
.
У механіці суттєвим є приріст потенціальної енергії, а не початок її відліку, а тому коли кажуть про величину потенціальної енергії, то розуміють величину її приросту.
Розглянуті сили є центральними і консервативними. Перше пов'язане з тим, що вектори сил лежать на прямій, що з'єднує центри тіл, а друге пов'язане з тим, що їх робота не залежить від шляху, а визначається початковим "1" та кінцевим "2" положенням тіла. Дійсно з (6) можна записати
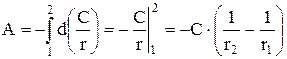 . (13)
. (13)
Вираз (13) і показує консеративність вказаних сил, які створюють потенціальну енергію.
Якщо робота сил залежить від шляху то такі сили називають дисипативними, наприклад, сили тертя. Робота таких сил призводить до втрати тілом енергії, шляхом переходу її у внутрішню теплову енергію. Механічні системи тіл, енергія яких перетворюється у інші не механічні види енергії, називаються дисипативними системами. Усі реальні механічні системи практично є дисипативними.
2.7.3. Робота зовнішньої сили. Механічна енергія
Під дією зовнішньої сили, відокремлене від інших тіл та силового поля тіло, придбає швидкість 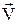 . При цьому потрібно встановити, у що реалізується робота сили. Для рішення цієї задачі помножимо скалярно праву та ліву частини рівняння Ньютона
. При цьому потрібно встановити, у що реалізується робота сили. Для рішення цієї задачі помножимо скалярно праву та ліву частини рівняння Ньютона 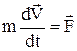 на відповідні частини переміщення тіла
на відповідні частини переміщення тіла 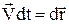 . В результаті ліворуч одержимо
. В результаті ліворуч одержимо
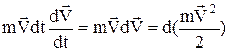 , (1)
, (1)
а праворуч
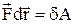 .
.
Таким чином одержуємо
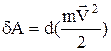 ,
,
що робота зовнішньої сили, йде на приріст деякої величини
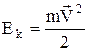
яку назвають кінетичною енергією тіла.
Отже, знаходячись у силовому полі, тіло може мати як потенціальну, так і кінетичну енергію. Сума цих енергій складає повну механічну енергіютіла чи системи тіл
E=Eк+Еп.
2.7.4. Закон збереження енергії
Закон збереження енергії:величина повної механічної енергії замкненої системи з консервативними силами взаємодії, що є сумою потенціальної та кінетичної енергій Ek+Eп, зберігається, тобто Е=Ek+Eп=const у будь-який момент часу, до і після будь-яких внутрішніх взаємодій між складовими системи.
Запишемо рівняння руху і-го тіла консервативної системи з N тіл у загальному виді:
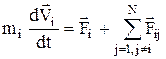 , (1)
, (1)
де 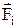 ¾ зовнішня сила,
¾ зовнішня сила, 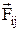 ¾ сила внутрішньої дії j-го тіла. Помножимо скалярно ліву та праву частини рівняння відповідно на ліву та праву частини виразу для переміщення
¾ сила внутрішньої дії j-го тіла. Помножимо скалярно ліву та праву частини рівняння відповідно на ліву та праву частини виразу для переміщення 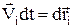
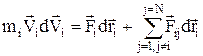 ,
,
і далі
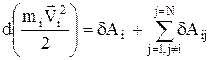 . (2)
. (2)
В (2)
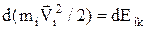 (3)
(3)
¾приріст кінетичної енергії,
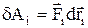 (4)
(4)
¾ елементарна робота зовнішньої сили,
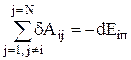 . (5)
. (5)
¾ робота внутрішніх сил, яка виконується за рахунок зменшення потенціальної енергії тіла 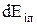 .
.
Тепер, використовуючи (3-5), (2) можна записати таким чином
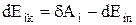 ,
,
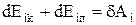 ,
,
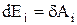 . (6)
. (6)
В (6)
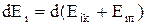
¾ приріст повної механічної енергії і-го тіла.
Узявши в (6) суму по усім тілам системи, одержимо
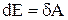 ,
,
де Е ¾ повна механічна енергія системи, dА ¾ робота зовнішніх сил над системою. Якщо система тіл замкнена, тобто усі 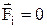 , то dА=0 і Е=const¾енергія замкненої системи тіл зберігається.
, то dА=0 і Е=const¾енергія замкненої системи тіл зберігається.
2.8. Пружні деформації
2.8.1. Пружна деформація, закон Гука
Пружна сила. Під дією зовнішньої сили в тілі виникають деформації, які створюють сили протидії. Деформації називаються пружними, якщо вони зникають після припинення дії зовнішньої сили, а внутрішні сили протидії у цьому випадкові називаються пружними силами. Прикладом пружних сил є сили, що виникають при незначних розтягуваннях пружини. При цьому величина пружної сили 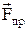 пропорційна величині приросту довжини пружини
пропорційна величині приросту довжини пружини
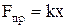 , (1)
, (1)
де k - коефіцієнт жорсткості пружини, х - видовження пружини. Напрямок пружної сили завжди такий, що протидіє деформації.
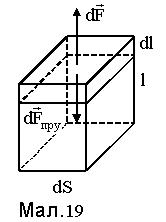 Напругою s називається величина, яка чисельно дорівнює пружній силі, що приходиться на одиницю площі перерізу тіла (див. Мал.19)
Напругою s називається величина, яка чисельно дорівнює пружній силі, що приходиться на одиницю площі перерізу тіла (див. Мал.19)
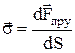 . (2)
. (2)
Вона може мати нормальну та тангенціальну до dS складові.
Закон Гука: напруга s при пружній деформації твердого тіла прямо пропорційна відносній деформації 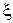
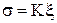 , (3)
, (3)
де K ¾ модуль пружності. При односторонньому стисненні (розтягуванні) змінюється довжина тіла x=l на величину dx=dl, що створює відносну деформацію 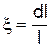 . Модуль пружності K є модулем Юнга E, який чисельно дорівнює напрузі, при якій тіло видовжується у двоє.
. Модуль пружності K є модулем Юнга E, який чисельно дорівнює напрузі, при якій тіло видовжується у двоє.
Відносний поздовжній розтяг (стиснення) 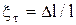 призводить до відносного поперечного звуження (розширення)
призводить до відносного поперечного звуження (розширення) 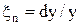 , де y ¾ поперечний розмір тіла. Відношення відносного поперечного звуження до відносного видовження
, де y ¾ поперечний розмір тіла. Відношення відносного поперечного звуження до відносного видовження 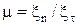 називається коефіцієнтом Пуассона.
називається коефіцієнтом Пуассона.
Сила пружності, яка діє на тіло з боку опори або підвісу, називається реакцією опори або силою натягу підвісу. Якщо сила, що діє на тіло, пропорційна зміщенню тіла зі стану рівноваги, то вона називається квазипружною.
Застосуємо закон Гука до пружної деформації пружини довжиною L. Пружна деформація створює в пружині напруженість
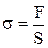 , (3)
, (3)
де F - величина пружної сили, S - площа перерізу пружини. При відносному видовженні 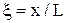 закон Гука запишеться у вигляді
закон Гука запишеться у вигляді
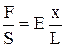 . (4)
. (4)
З (1) і (4) одержимо вираз для коефіцієнт жорсткості пружини
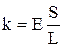 (5)
(5)
2.8.1.1. Енергія пружної деформації
Розглянемо розтягнення циліндричного зразка з площею основи S. При дії нормальної до основи сили F, зміщення основи на x викликає появу пружної сили
Fп=kx,
де k ¾ коефіцієнт пружності. При подальшому зміщенні поверхні S на величину dx силою 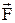 виконується робота dA проти пружної сили. Ця робота йде на приріст енергії деформації W: dA=dW. З очевидних співвідношень маємо:
виконується робота dA проти пружної сили. Ця робота йде на приріст енергії деформації W: dA=dW. З очевидних співвідношень маємо:
dA=Fпdx= 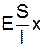 ·dx
·dx
W= 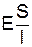
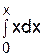 , W=
, W= 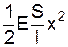 =
= 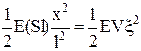 , (1)
, (1)
де V=Sl ¾ об’єм тіла.
Уведемо густину енергії пружної деформації 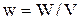 і з (1) одержимо
і з (1) одержимо
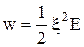 . (2)
. (2)
2.9. Ступені свободи, узагальнені координати
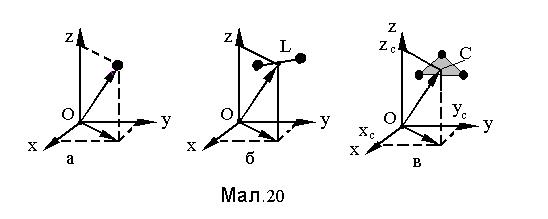 |
Ступені свободи (вільності) тіла ¾ незалежні параметри, які визначають його положення в просторі. Розрізняють поступальні (поступальний рух), обертові (обертовий рух) та коливальні (коливальний рух) ступені свободи. Точкове тіло має 3 поступальні ступені свободи nпост, наприклад, три просторові координати x,y,z (див.Мал.20 а). Система з двох точкових вільних частинок має 6 поступальних ступенів свободи. Якщо ж їх жорстко зв'язати на відстані L (див.Мал.20 б) одна від другої, то можна ввести рівняння зв'язку
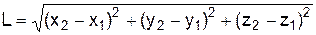 . (1)
. (1)
Тепер будь-який з 6 параметрів 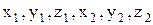 можна виразити через 5 інших і незалежних параметрів стане на 1 менше. Це означає, що кожне з рівнянь зв'язку зменшує число незалежних параметрів на 1. Зв'язки¾це рівняння, які описують обмеження руху тіла іншими тілами системи.Узагалі можна покласти, що система N жорстко зв'язаних тіл має 3 поступальні ступені свободи
можна виразити через 5 інших і незалежних параметрів стане на 1 менше. Це означає, що кожне з рівнянь зв'язку зменшує число незалежних параметрів на 1. Зв'язки¾це рівняння, які описують обмеження руху тіла іншими тілами системи.Узагалі можна покласти, що система N жорстко зв'язаних тіл має 3 поступальні ступені свободи 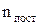 , які визначають положення її центра мас C у просторі (див.Мал.20 в), та 3 обертові ступені свободи nоберт ¾ кути a, b, g, що визначають орієнтацію системи відносно осей OX,OY,OZ. Інші ступені свободи 3n×(
, які визначають положення її центра мас C у просторі (див.Мал.20 в), та 3 обертові ступені свободи nоберт ¾ кути a, b, g, що визначають орієнтацію системи відносно осей OX,OY,OZ. Інші ступені свободи 3n×( 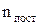 + nоберт) зникають у зв'язках. Якщо між тілами замість жорстких зв'язків установлюються пружні , то вони стають коливальними ступенями свободи
+ nоберт) зникають у зв'язках. Якщо між тілами замість жорстких зв'язків установлюються пружні , то вони стають коливальними ступенями свободи
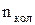 =3n-(
=3n-( 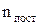 + nоберт) . (2)
+ nоберт) . (2)
Зв'язки між атомами в молекулі, наприклад, води Н2О при кімнатних температурах можна вважати жорсткими, тому що при таких температурах теплової енергії замало для збурення коливань між атомами. При високих температурах такі збурення можуть відбуватися і зв'язки стануть коливальними ступенями свободи. Якщо система є лінійною, то в (2) 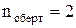 .
.
Наявність зв'язків зменшує число ступенів свободи на їх кількість.
Незалежні параметри q1, q2, ..., qs, які задають положення системи тіл із s ступенями свободи, називаються узагальненими координатами.
Дата добавления: 2015-09-18; просмотров: 13799;
