Маятник Обербека

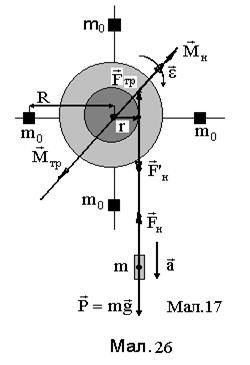Для ілюстрації сумісного рішення рівнянь поступального та обертового руху, розглянемо маятник Обербека, який являє собою циліндричне тіло із шківом на осі радіусу r та 4-ма однаковими взаємно перпендикулярними стержнями. На стержнях пристосовані пересувні тягарці масою m₀ кожний. Вони розташовані на відстані R від центру маятника (див.Мал. 26).

Стержні лежать у площині ^ осі циліндра і проходять через центр маятника. Маятник приводиться в обертовий рух тягарцем m із ниткою, намотаною на шків. Вісь обертання співпадає з віссю циліндра. Спочатку тягарець за рахунок сили натягу нитки 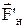розкручує маятник на всю довжину нитки h₁ і в нижній точці ривком маятника починає підніматися в гору. Після підняття тягарця на висоту h₂<h₁, маятник зупиняється й починає обертовий рух у протилежному початковому напрямкові.

За час опускання t та підйому t¢ маятник повертається на кут

,

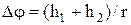де r ¾ радіус шківа. Запишемо рівняння руху тягарця та маятника, виходячи з наступного. При опусканні тягарця, маятник приводиться в обертовий рух моментом сили натягу 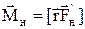, де ¾радіус-вектор точки прикладання сили відносно центра обертання, а момент сили тертя 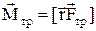гальмує цей рух (див. Мал. 17). Вектор кутового прискорення 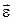лежить на осі обертання і 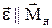, причому 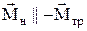. Усі три вектори 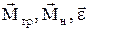лежать на осі обертання і тому, вибравши напрям вектора кутового прискорення за додатній, векторне рівняння другого закону Ньютона для обертового руху маятника

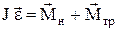
можна записати в алгебраїчному вигляді

.

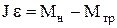В цьому рівнянні 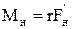¾ модуль моменту сили натягу підвісу.

При опусканні тягарця, на нього діють прискорююча сила тяжіння 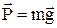та гальмуюча сила натягу 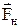, причому 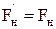. Вектор прискорення 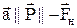. Усі три вектори лежать на одній прямій і тому, вибравши за додатній напрямок вектора прискорення, векторне рівняння другого закону Ньютона для прискореного руху тягарця

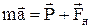
можна записати в алгебраїчному вигляді

.

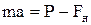Таким чином ми одержали першу пару рівнянь руху маятника Обербека:

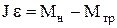, (1)

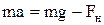_. (2)

Рух тягарця рівноприскорений і тому

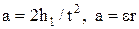. (3)

Для знаходження моменту інерції маятника J, помножимо рівняння (2) на r і додамо ліві та праві частини рівнянь (1-2). В результаті одержимо

rmg- 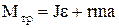. (4)

Підставимо в (4) 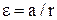і знайдемо J:

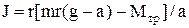. (5)

В (5) залишається невідомим момент сили тертя. Знайдемо його з того, що робота проти сили тертя дорівнює

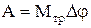, (6)

Робота виконується за рахунок зменшення потенціальної енергії тягарця на величину 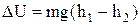. Після підстановки в (6) значень кута повороту та енергії одержимо значення моменту сили тертя

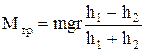. (7)

Момент інерції J є сумою моменту інерції власне маятника J₀ та моменту інерції 4-х тягарців m, які можна вважати точковими, і тоді

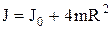. (8)

2.15. Силові поля. Зв’язок сили та потенціальної енергії

Якщо в деякому просторі виникають сили, що діють на розміщене там тіло, то кажуть, що в цьому просторі існує силове поле. Силове поле називається стаціонарним, якщо сила поля не залежить від часу.

Діючи на тіло, сила поля може перемістити його на 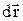, виконавши елементарну роботу

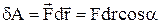, (1)

де a ¾ кут між векторами сили та переміщення. Якщо при переміщенні тіла з точки 1 у точку 2, робота сил поля не залежить від того, яким шляхом здійснюється переміщення, а визначається початковим і кінцевим положенням тіла, то такі сили називаються консервативними, а їх поля потенціальними.

Доведемо, що робота консервативних сил на замкненому шляху дорівнює нулю. Дійсно, якщо замкнений контур С розділити на дві частини 1а2 та 2б1 (див. Мал. 27), то роботу на цьому шляху можна записати як 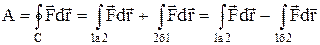. В останньому виразі ми врахували, що на шляху 1б2 переміщення 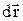змінює свій напрямок на протилежний відносно руху в напрямку 2б1. Для консервативних сил 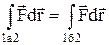і тоді А=0.

Силове поле можна представити графічно за допомогою силових ліній. Це уявні лінії, дотична до яких задає напрямок сили. Силові лінії не перетинаються (у противному в точці перетину було б 2 напрями однієї сили), а їх густина в поперечному перерізі чисельно дорівнює величині сили.

Центральниминазиваються сили, що залежать від відстані між взаємодіючими тілами і лежать на прямій, яка з’єднує центри тіл. До таких сил належать сили гравітаційної та електростатичної взаємодії точкових тіл, які можна представити у вигляді 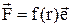, де r ¾ відстань між тілами, 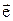¾одиничний вектор напрямку сили. Роботу таких сил ми розглянули вище і показали, що 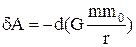для гравітаційної взаємодії та 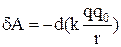для кулонівської взаємодії, тобто робота виконується за рахунок зменшення деякої величини U(r). Ця величина залежить від взаємного розташування взаємодіючих тіл, і ми назвали її потенціальною енергією. Потенціальна енергія U визначається з точністю до деякої довільної сталої, але фізичний зміст має лише її приріст DU=U₂-U₁ чи убуток DU=-( U₂-U₁), в яких ця довільна стала випадає. У зв'язку з цим у виразах для U сталу опускають.

Енергетичною характеристикою гравітаційного силового поля є його потенціалj, який чисельно дорівнює потенціальній енергії тіла одиничної маси

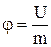, (2)

або в явному виді

.

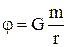Для електростатичного поля, створеного точковим зарядом q маємо

.

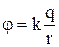Відповідно силовою характеристикою поля є напруженістьполя, яка чисельно дорівнює силі, що діє на одиничну масу 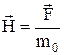для гравітаційного поля і 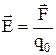для електростатичного поля. У наведених виразах m₀ та q₀ є точкові пробні маса та заряд, величина яких не деформує досліджуване силове поле. Для поля, створеного точковою масою m, величина напруженості поля 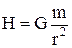, а в умовах Землі при поверхні вона дорівнює величині прискорення вільного падіння 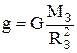. Для електростатичного поля, створеного точковим зарядом q, дорівнює 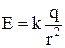. Поверхня, що є геометричним місцем точок з однаковим потенціалом називається еквіпотенціальною.

Робота поля (1) виконується за рахунок потенціальної енергії поля, тобто dА=-dU і, враховуючи (2), одержимо

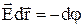(3)

для електричного поля та

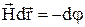(4)

для гравітаційного поля. Вирази (3-4) є диференціальними рівняннями, що зв'язують силові та енергетичні характеристики поля.

По заданій функції потенціальної енергії U(r) можна встановити сили, що створюють це поле. Справді, якщо робота поля виконується за рахунок убутку потенціальної енергії взаємодіючих тіл, то

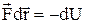. (5)

Якщо переміщення здійснюється вздовж осі ОХ, то

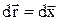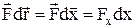i . (6)

З (5) та (6) одержимо

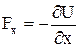. (7)

Аналогічно можна одержати

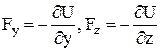. (8)

Тепер силу представимо в такому вигляді:

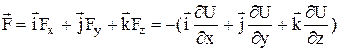. (9)

Якщо ввести векторний математичний оператор градієнта

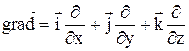, (10)

то

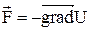. (11)

Якщо розділити ліву та праву частини одержаного виразу на величину, що генерує цю силу, то одержимо вираз, що визначає напруженість поля через його потенціал, наприклад, для електростатичного поля

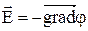. (12)

Якщо розглянути переміщення 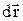тіла вздовж еквіпотенціальної поверхні (по дотичній до неї), то dU=0, При цьому 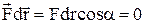, тобто кут a між напрямком сили та еквіпотенціальною поверхнею дорівнює 90⁰ і сила (напруженість поля) ^ еквіпотенціальній поверхні.

2.16. Рівновага в механіці

Станом рівноваги тіла є стан, в якому рівнодійні сил та моментів сил, що діють на тіло, дорівнюють нулю.

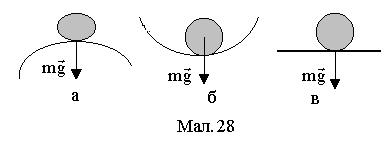
Якщо при елементарному зміщенні тіла зі стану рівноваги виникають сили, які сприяють подальшому зміщенню (див.Мал.28а), то такий стан рівноваги називається нестійким.

Якщо при елементарному зміщенні тіла зі стану рівноваги виникають сили, які протидіють подальшому зміщенню (див.Мал.28б), то такий стан рівноваги називається стійким.

Якщо при елементарному зміщенні тіла зі стану рівноваги не виникають сили (див.Мал.28 в), які сприяють або протидіють подальшому зміщенню, то такий стан рівноваги називається невиразним (невизначеним).

Положенню стійкої рівноваги тіла відповідає мінімум потенціальної енергії.

2.17. Механіка руху рідини

Тиск сили 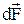на поверхню рідини dS визначається силою, що діє по нормалі до неї

,

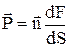де 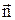¾ одиничний вектор нормалі до dS.

Закон Паскалястверджує, що рідина або газ передає тиск в усіх напрямках однаково.

Закон Архімедастверджує, що на тіло, занурене в рідину або газ, діє виштовхувальна сила, рівна за величиною вазі витісненої рідини або газу, і прикладена в точці тіла, яка співпадає з центром мас витісненої рідини або газу. Сила Архімеда має напрямок протилежний напрямкові сили тяжіння Землі.

В механіці рідину вважають як суцільне середовище, густина якого не залежить від тиску. Рух рідини називають течією, а саму рідину, що рухається потоком. У випадку усталеного потоку рідини виділяють лініюпотоку, яка є уявною кривою, дотична до якої у кожній її точці співпадає за напрямком із вектором швидкості рідини 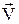в цій точці. Трубка потоку¾ це поверхня, утворена лініями потоку, які проведені через усі точки замкнутого контуру. Частина потоку, обмежена трубкою потоку, називається струменем. На дотичній до струменю лежить вектор швидкості рідини 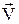. Ідеальнарідина ¾ це рідина, в якій відсутня сила опору (сила внутрішнього тертя - в'язкість) між окремими шарами рідини, що рухаються.

Нехай струмінь рідини з густиною r має в основах перпендикулярних перерізів площі dS₁ i dS₂ величини швидкостей V₁ та V₂. В усталеній течії потік рідини нерозривний: кількість рідини (маса) rV₁S₁, що проходить за одиницю часу через переріз S₁, дорівнює кількості рідини rV₂S₂, що проходить за одиницю часу через переріз S₂. Математично це записується у вигляді рівняння нерозривності:

.

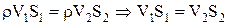Перерізи в трубці потоку можуть вибиратися довільно, а тому рівняння нерозривностіпотоку рідини в струмені можна записати у вигляді

VS=const.

2.18. Рівняння Бернуллі

В момент часу t виділимо в ідеальній рідині трубку потоку з частиною рідини між перерізами dS₁ i dS₂ (див. Мал. 29). Під дією сил тиску dF₁ i dF₂ та сили тяжіння за час dt ця рідина переміститься й займе об'єм між перерізами 1' та 2'. При цьому переміщення рідини за час dt у першому перерізі становитиме 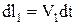, а у другому- 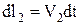. Робота сил dA по переміщенню рідини йде на зміну кінетичної dE_k та потенціальної dE_п енергії рідини

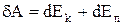. (1)

Роботу можна записати у вигляді

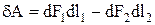, (2)

або після підстановки величин сил тиску та переміщень одержимо

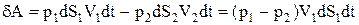, (3)

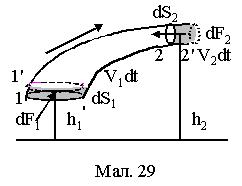
де р₁, р₂ тиски, V₁, V₂ ¾ швидкості в перерізах 1 та 2, а 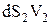замінено на 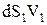згідно рівняння нерозривності рідини.

Зміна кінетичної енергії становить

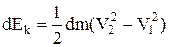, (4)

а потенціальної

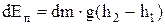, (5)

де

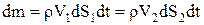¾ маса рідини між перерізами 1-1' або 2-2', а 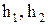¾ висоти центрів мас рідини dm у цих перерізах. Підставляючи вирази для роботи та енергій у рівняння (1), одержимо 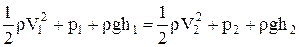(6)

Перерізи 1 та 2 вибрані довільно, тому в загальному вигляді можна записати

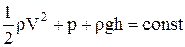. (7)

де р ¾ статичний тиск, що діє на стінки трубки, а 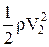¾ динамічний тиск, що діє на поверхню площини в течії рідини. Рівняння (7) називається рівнянням Бернуллі.

2.19. Контрольні питання

І. Що є джерелом механічного руху? Який фізичний зміст сили?

2. Що таке рівнодійна сил та як вона знаходиться, наведіть приклад?

3. Перший закон Ньютона, що визначає цей закон?

4. Другий закон Ньютона і його фізичний зміст.

5. Який фізичний зміст вкладається в поняття маса тіла та адитивність маси?

6. Що таке імпульс сили? Як записати рівняння другого закону Ньютона через імпульс?

7. Що означає імпульс сили та який його зв'язок з імпульсом тіла?

8. У чому полягає принцип суперпозиції сил?

9. Третій закон Ньютона.

10. Виведіть закон збереження імпульсу замкненої системи з 3 тіл, для N тіл.

11. Як визначається радіус-вектор положення центра мас системи тіл.

12. Знайдіть швидкість центра мас та його рівняння руху.

13. Які властивості руху центра мас замкненої системи тіл?

14. Які сили у природі Ви знаєте? Запишіть формули та вкажіть особливості цих сил.

15. Виведіть рівняння Мещерського, поясніть фізичний зміст величин, які входять до цього рівняння.

16. Від яких величин залежить реактивна сила?

17. Виведіть формулу Ціолковського.

18. Перетворення координат Галілея та механічний принцип відносності.

19. Наведіть приклади неінерційних систем.

20. Визначте динамічні характеристики обертального ру­ху матеріальної точки, абсолютно твердого тіла: момент сили, момент імпульсу; як знайти їх величину й напрямок.

21. Що таке пара сил? Як знайти момент пари сил?

22. Яка умова рівноваги тіла, що обертається?

23. Визначить момент інерції матеріальної точки, макроскопічного тіла.

24. Розрахуйте момент інерції однорідного тіла правильної геомет­ричної форми відносно осі, що проходить через центр мас: обруча, тонкостінного циліндра, диска, стержня.

25. Наведіть та дайте фізичний зміст теореми Штейнера. Наведіть приклад застосування.

26. Виведіть основне рівняння динаміки обертального руху тіла.

27. Виведіть закон збереження моменту імпульсу замкненої системи з 3 тіл, для N тіл.

28. Проведіть аналогії між законами динаміки для поступального руху та для обертального руху.

29. Наведіть формули сил у природі: гравітаційної сили, кулонівської сили, пружної сили, сили опору, сили тертя.

30. Дайте визначення та аналіз елементарної роботи та потужності в механіці.

31. Дайте визначення коефіцієнта корисної дії.

32. Знайдіть величину елементарної роботи: гравітаційної сили, кулонівської сили, пружної сили, сили опору, сили тертя.

33. Виведіть рівняння для розрахунку повної роботи при обертовому русі.

34. Дайте графічне тлумачення роботи сили.

35. Що являє собою енергія тіла та системи взаємодіючих тіл у механіці?

36. Знайдіть зв'язок елементарної роботи сили по переміщенню відокремленого тіла та кінетичною енергією.

37. Виведіть формулу кінетичної енергії тіла, що обертається.

38. Які бувають види енергії у механіці?

39. Доведіть закон збереження механічної енергії.

40. Дайте розв'язок задачі про центральний удар двох куль.

41. Запишіть рівняння руху маятника Обербека та знайдіть його розв'язок.

42. Дайте загальні визначення поняттям: потенціальна енергія; консер­вативна сила; потенціальне поле

43. Дайте загальне визначення напруженості силового поля та потенціалу.

44. Виведіть зв'язок силової та енергетичної характеристик поля.

45. Знайдіть вираз для сили поля через потенціальну енергію.

46. Що означає рівність 0 циркуляції напруженості поля?

47. Сформулюйте закони Паскаля та Архімеда.

48. Визначить поняття: течія, потік, лінія потоку, трубка потоку та струмінь.

49. Дайте визначення ідеальної рідини.

50. Знайдіть рівняння нерозривності рідини.

51. Виведіть рівняння Бернуллі.

52. Який фізичний зміст статичного та динамічного тиску?